

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Apéry Number
المؤلف:
Beukers, F.
المصدر:
"Some Congruences for the Apéry Numbers." J. Number Th. 21
الجزء والصفحة:
...
29-12-2020
1096
Apéry's numbers are defined by
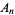 |
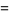 |
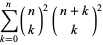 |
(1) |
 |
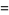 |
![sum_(k=0)^(n)([(n+k)!]^2)/((k!)^4[(n-k)!]^2)](https://mathworld.wolfram.com/images/equations/AperyNumber/Inline6.gif) |
(2) |
 |
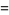 |
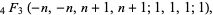 |
(3) |
where 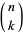 is a binomial coefficient. The first few for
is a binomial coefficient. The first few for 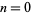 , 1, 2, ... are 1, 5, 73, 1445, 33001, 819005, ... (OEIS A005259).
, 1, 2, ... are 1, 5, 73, 1445, 33001, 819005, ... (OEIS A005259).
The first few prime Apéry numbers are 5, 73, 12073365010564729, 10258527782126040976126514552283001, ... (OEIS A092826), which have indices 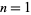 , 2, 12, 24, ... (OEIS A092825).
, 2, 12, 24, ... (OEIS A092825).
The 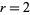 case of Schmidt's problem expresses these numbers in the form
case of Schmidt's problem expresses these numbers in the form
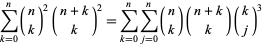 |
(4) |
(Strehl 1993, 1994; Koepf 1998, p. 55).
They are also given by the recurrence equation
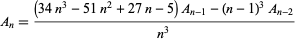 |
(5) |
with 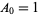 and
and 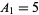 (Beukers 1987).
(Beukers 1987).
There is also an associated set of numbers
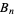 |
 |
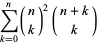 |
(6) |
 |
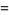 |
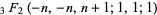 |
(7) |
(Beukers 1987), where 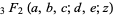 is a generalized hypergeometric function. The values for
is a generalized hypergeometric function. The values for 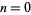 , 1, ... are 1, 3, 19, 147, 1251, 11253, 104959, ... (OEIS A005258). The first few prime
, 1, ... are 1, 3, 19, 147, 1251, 11253, 104959, ... (OEIS A005258). The first few prime 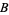 -numbers are 5, 73, 12073365010564729, 10258527782126040976126514552283001, ... (OEIS A092827), which have indices
-numbers are 5, 73, 12073365010564729, 10258527782126040976126514552283001, ... (OEIS A092827), which have indices 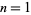 , 2, 6, 8, ... (OEIS A092828), with no others for
, 2, 6, 8, ... (OEIS A092828), with no others for 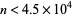 (Weisstein, Mar. 8, 2004).
(Weisstein, Mar. 8, 2004).
The 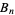 numbers are also given by the recurrence equation
numbers are also given by the recurrence equation
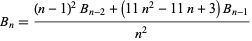 |
(8) |
with 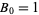 and
and 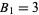 .
.
Both 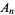 and
and 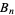 arose in Apéry's irrationality proof of
arose in Apéry's irrationality proof of 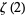 and
and 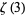 (van der Poorten 1979, Beukers 1987). They satisfy some surprising congruence properties,
(van der Poorten 1979, Beukers 1987). They satisfy some surprising congruence properties,
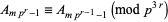 |
(9) |
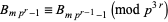 |
(10) |
for 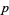 a prime
a prime 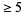 and
and 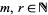 (Beukers 1985, 1987), as well as
(Beukers 1985, 1987), as well as
|
(11) |
(Stienstra and Beukers 1985, Beukers 1987). Defining 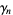 from the generating function
from the generating function
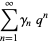 |
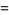 |
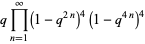 |
(12) |
 |
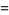 |
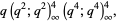 |
(13) |
where 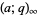 is a q-Pochhammer symbol, gives
is a q-Pochhammer symbol, gives 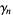 of 1,
of 1, 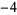 ,
, 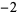 , 24,
, 24, 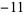 ,
, 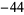 , ... (OEIS A030211; Koike 1984) for
, ... (OEIS A030211; Koike 1984) for 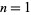 , 3, 5, ..., and
, 3, 5, ..., and
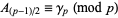 |
(14) |
for 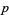 an odd prime (Beukers 1987). Furthermore, for
an odd prime (Beukers 1987). Furthermore, for 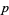 an odd prime and
an odd prime and 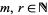 ,
,
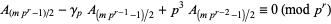 |
(15) |
(Beukers 1987).
The Apéry numbers are given by the diagonal elements 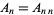 in the identity
in the identity
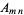 |
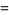 |
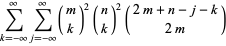 |
(16) |
 |
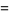 |
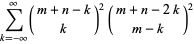 |
(17) |
 |
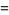 |
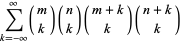 |
(18) |
(Koepf 1998, p. 119).
REFERENCES:
Apéry, R. "Irrationalité de 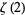 et
et 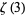 ." Astérisque 61, 11-13, 1979.
." Astérisque 61, 11-13, 1979.
Apéry, R. "Interpolation de fractions continues et irrationalité de certaines constantes." Mathématiques, Ministère universités (France), Comité travaux historiques et scientifiques. Bull. Section Sciences 3, 243-246, 1981.
Beukers, F. "Some Congruences for the Apéry Numbers." J. Number Th. 21, 141-155, 1985.
Beukers, F. "Another Congruence for the Apéry Numbers." J. Number Th. 25, 201-210, 1987.
Chowla, S.; Cowles, J.; and Cowles, M. "Congruence Properties of Apéry Numbers." J. Number Th. 12, 188-190, 1980.
Gessel, I. "Some Congruences for the Apéry Numbers." J. Number Th. 14, 362-368, 1982.
Koepf, W. "Hypergeometric Identities." Ch. 2 in Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 29 and 119, 1998.
Koike, M. "On McKay's Conjecture." Nagoya Math. J. 95, 85-89, 1984.
Schmidt, A. L. "Legendre Transforms and Apéry's Sequences." J. Austral. Math. Soc. Ser. A 58, 358-375, 1995.
Sloane, N. J. A. Sequences A005258/M3057, A005259/M4020, A030211, A092825, A092826, A092827, and A092828 in "The On-Line Encyclopedia of Integer Sequences."
Stienstra, J. and Beukers, F. "On the Picard-Fuchs Equation and the Formal Brauer Group of Certain Elliptic  Surfaces." Math. Ann. 271, 269-304, 1985.
Surfaces." Math. Ann. 271, 269-304, 1985.
Strehl, V. "Binomial Sums and Identities." Maple Technical Newsletter 10, 37-49, 1993.
Strehl, V. "Binomial Identities--Combinatorial and Algorithmic Aspects." Discrete Math. 136, 309-346, 1994.
van der Poorten, A. "A Proof that Euler Missed... Apéry's Proof of the Irrationality of 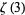 ." Math. Intel. 1, 196-203, 1979.
." Math. Intel. 1, 196-203, 1979.