Rabbit Constant
المؤلف:
Anderson, P. G.; Brown, T. C.; and Shiue, P. J.-S.
المصدر:
"A Simple Proof of a Remarkable Continued Fraction Identity." Proc. Amer. Math. Soc. 123
الجزء والصفحة:
...
8-12-2020
1471
Rabbit Constant
The limiting rabbit sequence written as a binary fraction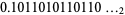 
(OEIS A005614), where 
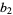denotes a binary number (a number in base-2). The decimal value is
 |
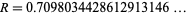(1)
|
(OEIS A014565).
Amazingly, the rabbit constant is also given by the continued fraction [0;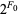 
, 
, 
, 
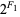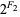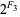, ...] = [2, 2, 4, 8, 32, 256, 8192, 2097152, 17179869184, ...] (OEIS A000301), where 
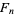are Fibonacci numbers with 
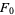taken as 0 (Gardner 1989, Schroeder 1991). Another amazing connection was discovered by S. Plouffe. Define the Beatty sequence ![<span style=]()
{a_i}" src="https://mathworld.wolfram.com/images/equations/RabbitConstant/Inline9.gif" style="height:15px; width:21px" /> by
 |
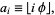(2)
|
where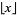 
is the floor function and 
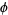is the golden ratio. The first few terms are 1, 3, 4, 6, 8, 9, 11, ... (OEIS A000201). Then
 |
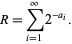(3)
|
This is a special case of the Devil's staircase function with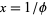 
.
The irrationality measure of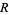 
is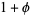 
(D. Terr, pers. comm., May 21, 2004).
REFERENCES:
Anderson, P. G.; Brown, T. C.; and Shiue, P. J.-S. "A Simple Proof of a Remarkable Continued Fraction Identity." Proc. Amer. Math. Soc. 123, 2005-2009, 1995.
Finch, S. R. "Prouhet-Thue-Morse Constant." §6.8 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 436-441, 2003.
Gardner, M. Penrose Tiles and Trapdoor Ciphers... and the Return of Dr. Matrix, reissue ed. New York: W. H. Freeman, pp. 21-22, 1989.
Schroeder, M. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, p. 55, 1991.
Sloane, N. J. A. Sequences A000301, A000201/M2322, A005614, and A014565 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
