Complete Sequence
المؤلف:
Brown, J. L. Jr.
المصدر:
"Unique Representations of Integers as Sums of Distinct Lucas Numbers." Fib. Quart. 7
الجزء والصفحة:
...
25-10-2020
1377
Complete Sequence
A sequence of numbers ![V=<span style=]()
{nu_n}" src="https://mathworld.wolfram.com/images/equations/CompleteSequence/Inline1.gif" style="height:15px; width:50px" /> is complete if every positive integer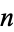 
is the sum of some subsequence of 
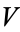, i.e., there exist 
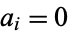or 1 such that
(Honsberger 1985, pp. 123-126). The Fibonacci numbers are complete. In fact, dropping one number still leaves a complete sequence, although dropping two numbers does not (Honsberger 1985, pp. 123 and 126). The sequence of primes with the element ![<span style=]()
{1}" src="https://mathworld.wolfram.com/images/equations/CompleteSequence/Inline5.gif" style="height:15px; width:17px" /> prepended,
![<span style=]() {1,2,3,5,7,11,13,17,19,23,...} " src="https://mathworld.wolfram.com/images/equations/CompleteSequence/NumberedEquation2.gif" style="height:15px; width:209px" /> |
is complete, even if any number of primes each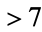 
are dropped, as long as the dropped terms do not include two consecutive primes (Honsberger 1985, pp. 127-128). This is a consequence of Bertrand's postulate.
REFERENCES:
Brown, J. L. Jr. "Unique Representations of Integers as Sums of Distinct Lucas Numbers." Fib. Quart. 7, 243-252, 1969.
Hoggatt, V. E. Jr.; Cox, N.; and Bicknell, M. "A Primer for Fibonacci Numbers. XII." Fib. Quart. 11, 317-331, 1973.
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., 1985.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
