Primorial
المؤلف:
Finch, S. R.
المصدر:
Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
الجزء والصفحة:
...
12-10-2020
1121
Primorial
Let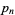 
be the 
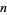th prime, then the primorial (which is the analog of the usual factorial for prime numbers) is defined by
 |
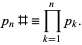(1)
|
The values of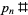 
for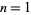 
, 2, ..., are 2, 6, 30, 210, 2310, 30030, 510510, ... (OEIS A002110).
It is sometimes convenient to define the primorial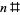 
for values other than just the primes, in which case it is taken to be given by the product of all primes less than or equal to 
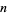, i.e.,
 |
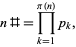(2)
|
where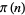 
is the prime counting function. For 
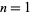, 2, ..., the first few values of 
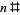are 1, 2, 6, 6, 30, 30, 210, 210, 210, 210, 2310, ... (OEIS A034386).
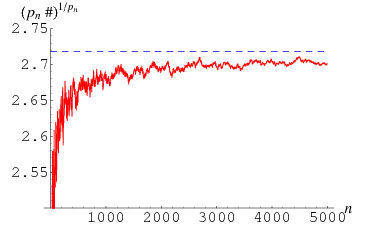
The logarithm of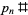 
is closely related to the Chebyshev function 
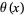, and a trivial rearrangement of the limit
 |
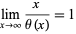(3)
|
gives
 |
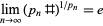(4)
|
(Ruiz 1997; Finch 2003, p. 14; Pruitt), where e is the usual base of the natural logarithm.
REFERENCES:
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
Pruitt, C. D. "A Theorem & Proof on the Density of Primes Utilizing Primorials." https://www.mathematical.com/mathprimorialproof.html.
Ruiz, S. M. "A Result on Prime Numbers." Math. Gaz. 81, 269, 1997.
Sloane, N. J. A. Sequence A002110/M1691 and A034386 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
