Cofactor
المؤلف:
Muir, T
المصدر:
A Treatise on the Theory of Determinants. New York: Dover,
الجزء والصفحة:
...
10-9-2020
1094
Cofactor
Given a factor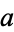 
of a number 
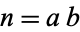, the cofactor of 
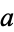is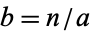 
.
A different type of cofactor, sometimes called a cofactor matrix, is a signed version of a minor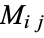 
defined by
and used in the computation of the determinant of a matrix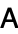 
according to
The cofactor can be computed in the Wolfram Language using
Cofactor[m_List?MatrixQ, {i_Integer, j_Integer}] :=
(-1)^(i+j) Det[Drop[Transpose[
Drop[Transpose[m], {j}]], {i}
]]
which is the equivalent of the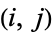 
th component of the CofactorMatrix defined below.
MinorMatrix[m_List?MatrixQ] :=
Map[Reverse, Minors[m], {0, 1}]
CofactorMatrix[m_List?MatrixQ] :=
MapIndexed[#1 (-1)^(Plus @@ #2)&,
MinorMatrix[m],{2}]
Cofactors can be computed using Cofactor[m, ![<span style=]()
{" src="https://mathworld.wolfram.com/images/equations/Cofactor/Inline8.gif" style="height:15px; width:5px" />i, j![<span style=]()
}" src="https://mathworld.wolfram.com/images/equations/Cofactor/Inline9.gif" style="height:15px; width:5px" />] in the Wolfram Language package Combinatorica` .
REFERENCES:
Lichtblau, D. "Symbolic FAQ." https://library.wolfram.com/infocenter/Conferences/325.
Muir, T. A Treatise on the Theory of Determinants. New York: Dover, p. 54, 1960.
Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, p. 235, 1990.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
