The quantities obtained from cubic, hexagonal, etc., lattice sums, evaluated at 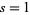, are called Madelung constants.

For cubic lattice sums

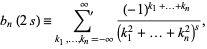(1)

the Madelung constants expressible in closed form for even indices 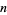, a few examples of which are summarized in the following table, where  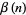is the Dirichlet beta function and  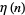is the Dirichlet eta function.

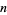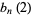		OEIS	constant
2		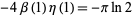A086054
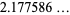4		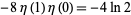A016639

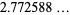To obtain the closed form for 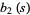, break up the double sum into pieces that do not include ,

	(2)
	(3)
	(4)

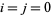where the negative sums have been reindexed to run over positive quantities. But 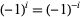, so all the above terms can be combined into

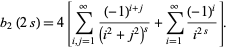(5)

The second of these sums can be done analytically as

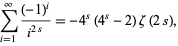(6)

which in the case 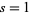 reduces to

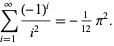(7)

The first sum is more difficult, but in the case 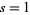 can be written

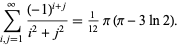(8)

Combining these then gives the original sum as

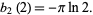(9)

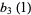 is given by Benson's formula (Borwein and Bailey 2003, p. 24)

			(10)
			(11)
			(12)

(OEIS A085469), where the prime indicates that summation over (0, 0, 0) is excluded.

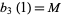 is sometimes called "the" Madelung constant, corresponds to the Madelung constant for a three-dimensional NaCl crystal. Crandall (1999) gave the expression

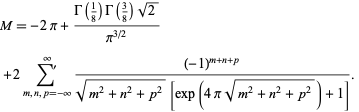(13)

Similar results were found by Tyagi (2004),

			(14)
			(15)
			(16)

the last of which converges rapidly. Averaging (16) and (13) then gives the beautiful equation

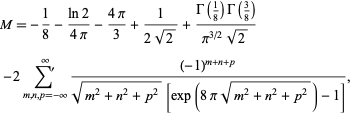(17)

which is correct to 10 decimal digits even if the sum is completely omitted (Tyagi 2004).

However, no closed form for 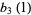 is known (Bailey et al. 2006).

For hexagonal lattice sums, 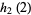 is expressible in closed form as

			(18)
			(19)

(OEIS A086055).

REFERENCES:

Bailey, D. H.; Borwein, J. M.; Crandall, R. E.; and Zucker, I. J. "Lattice Sums Arising from the Poisson Equation." J. Phys. A 46, 115201, 31 pp., 2013.

Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006.

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.

Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.

Buhler, J. and Wagon, S. "Secrets of the Madelung Constant." Mathematica in Education and Research 5, 49-55, Spring 1996.

Crandall, R. E. "New Representations for the Madelung Constant." Exp. Math. 8, 367-379, 1999.

Crandall, R. E. and Buhler, J. P. "Elementary Function Expansions for Madelung Constants." J. Phys. Ser. A: Math. and Gen. 20, 5497-5510, 1987.

Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.

Havil, J. "Madelung's Constant." §3.4 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 33-35, 2003.

Sloane, N. J. A. Sequences A016639, A085469, A086054, and A086055 in "The On-Line Encyclopedia of Integer Sequences."

Tyagi, S. "New Series Representation for Madelung Constant." Oct. 17, 2004. https://arxiv.org/abs/cond-mat/0410424.