Vector Spherical Harmonic
المؤلف:
Arfken, G.
المصدر:
"Vector Spherical Harmonics." §12.11 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
الجزء والصفحة:
...
25-9-2019
3493
Vector Spherical Harmonic
The spherical harmonics can be generalized to vector spherical harmonics by looking for a scalar function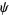 
and a constant vector 
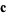such that
so
 |
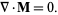(5)
|
Now interchange the order of differentiation and use the fact that multiplicative constants can be moving inside and outside the derivatives to obtain
and
Putting these together gives
![del ^2M+k^2M=del x[c(del ^2psi+k^2psi)],](http://mathworld.wolfram.com/images/equations/VectorSphericalHarmonic/NumberedEquation2.gif) |
(11)
|
so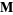 
satisfies the vector Helmholtz differential equation if 
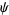satisfies the scalar Helmholtz differential equation
 |
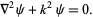(12)
|
Construct another vector function
 |
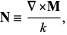(13)
|
which also satisfies the vector Helmholtz differential equation since
which gives
 |
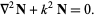(19)
|
We have the additional identity
In this formalism,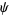 
is called the generating function and 
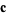is called the pilot vector. The choice of generating function is determined by the symmetry of the scalar equation, i.e., it is chosen to solve the desired scalar differential equation. If 
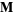is taken as
 |
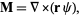(25)
|
where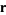 
is the radius vector, then 
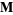is a solution to the vector wave equation in spherical coordinates. If we want vector solutions which are tangential to the radius vector,
so
 |
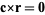(29)
|
and we may take
 |
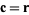(30)
|
(Arfken 1985, pp. 707-711; Bohren and Huffman 1983, p. 88).
A number of conventions are in use. Hill (1954) defines
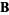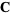Morse and Feshbach (1953) define vector harmonics called 
, 
, and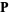 
using rather complicated expressions.
REFERENCES:
Arfken, G. "Vector Spherical Harmonics." §12.11 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 707-711, 1985.
Blatt, J. M. and Weisskopf, V. "Vector Spherical Harmonics." Appendix B, §1 in Theoretical Nuclear Physics. New York: Wiley, pp. 796-799, 1952.
Bohren, C. F. and Huffman, D. R. Absorption and Scattering of Light by Small Particles. New York: Wiley, 1983.
Hill, E. H. "The Theory of Vector Spherical Harmonics." Amer. J. Phys. 22, 211-214, 1954.
Jackson, J. D. Classical Electrodynamics, 2nd ed. New York: Wiley, pp. 744-755, 1975.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part II. New York: McGraw-Hill, pp. 1898-1901, 1953.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
