The 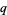-digamma function 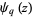, also denoted 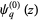, is defined as

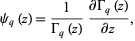(1)

where 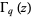 is the q-gamma function. It is also given by the sum

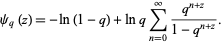(2)

The 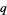-polygamma function  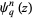(also denoted 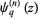) is defined by

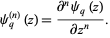(3)

It is implemented in the Wolfram Language as QPolyGamma[n, z, q], with the 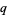-digamma function implemented as the special case QPolyGamma[z, q].

Certain classes of sums can be expressed in closed form using the 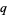-polygamma function, including

			(4)
			(5)

The 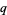-polygamma functions are related to the Lambert series

			(6)
			(7)
			(8)

(Borwein and Borwein 1987, pp. 91 and 95).

An identity connecting 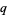-polygamma to elliptic functions is given by

(9)

where 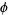 is the golden ratio and  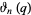is an Jacobi theta function.

REFERENCES:

Borwein, J. M. and Borwein, P. B. "Evaluation of Sums of Reciprocals of Fibonacci Sequences." §3.7 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 91-101, 1987.