Cylinder Function
المؤلف:
Watson, G. N.
المصدر:
A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.
الجزء والصفحة:
...
19-7-2019
1650
Cylinder Function
The cylinder function is defined as
![C(x,y)=<span style=]() {1 for sqrt(x^2+y^2)<=a; 0 for sqrt(x^2+y^2)>a. " src="http://mathworld.wolfram.com/images/equations/CylinderFunction/NumberedEquation1.gif" style="height:64px; width:196px" /> |
(1)
|
The Bessel functions are sometimes also called cylinder functions.
To find the Fourier transform of the cylinder function, let
and
Then
Let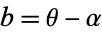 
, so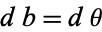 
. Then
where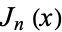 
is a Bessel function of the first kind.
As defined by Watson (1966), a "cylinder function" is any function which satisfies the recurrence relations
 |
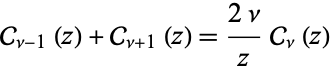(14)
|
 |
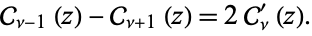(15)
|
This class of functions can be expressed in terms of Bessel functions.
REFERENCES:
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
