Hyperbolic Secant
المؤلف:
Abramowitz, M. and Stegun, I. A
المصدر:
"Hyperbolic Functions." §4.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
3-6-2019
2324
Hyperbolic Secant
The hyperbolic secant is defined as
where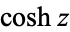 
is the hyperbolic cosine. It is implemented in the Wolfram Language as Sech[z].
On the real line, it has a maximum at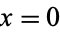 
and inflection points at 
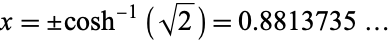(OEIS A091648). It has a fixed point at 
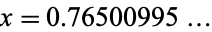(OEIS A069814).
The derivative is given by
 |
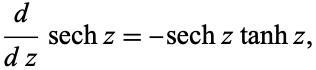(3)
|
where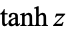 
is the hyperbolic tangent, and the indefinite integral by
![intsechzdz=2tan^(-1)[tanh(1/2z)]+C,](http://mathworld.wolfram.com/images/equations/HyperbolicSecant/NumberedEquation2.gif) |
(4)
|
where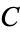 
is a constant of integration.
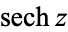has the Taylor series
(OEIS A046976 and A046977), where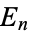 
is an Euler number and 
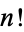is a factorial.
Equating coefficients of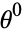 
, 
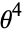, and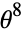 
in the Ramanujan cos/cosh identity
![[1+2sum_(n=1)^infty(cos(ntheta))/(cosh(npi))]^(-2)+[1+2sum_(n=1)^infty(cosh(ntheta))/(cosh(npi))]^(-2)=(2Gamma^4(3/4))/pi](http://mathworld.wolfram.com/images/equations/HyperbolicSecant/NumberedEquation3.gif) |
(7)
|
gives the amazing identities
![sum_(n=1)^inftysech(pin)=1/2<span style=]() {(sqrt(pi))/([Gamma(3/4)]^2)-1}
sum_(n=1)^inftyn^4sech(pin)=(18[Gamma(3/4)]^2)/(sqrt(pi))[sum_(n=1)^inftyn^2sech(pin)]^2
sum_(n=1)^inftyn^8sech(pin)=(168[Gamma(3/4)]^2)/(sqrt(pi))[sum_(n=1)^inftyn^2sech(pin)]×sum_(n=1)^inftyn^6sech(pin)-(63000[Gamma(3/4)]^6)/(pi^(3/2))[sum_(n=1)^inftyn^2sech(pin)]^4. " src="http://mathworld.wolfram.com/images/equations/HyperbolicSecant/NumberedEquation4.gif" style="height:230px; width:506px" /> |
(8)
|
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Hyperbolic Functions." §4.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 83-86, 1972.
Jeffrey, A. "Hyperbolic Identities." §2.5 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 117-122, 2000.
Sloane, N. J. A. Sequences A046976, A046977, A069814, and A091648 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Hyperbolic Secant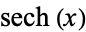 
and Cosecant 
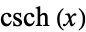Functions." Ch. 29 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 273-278, 1987.
Zwillinger, D. (Ed.). "Hyperbolic Functions." §6.7 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 476-481 1995.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
