Elliptic Integral of the First Kind
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Elliptic Integrals." Ch. 17 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
25-4-2019
5135
Elliptic Integral of the First Kind
Let the elliptic modulus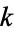 
satisfy 
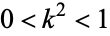, and the Jacobi amplitude be given by 
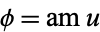with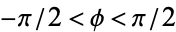 
. The incomplete elliptic integral of the first kind is then defined as
 |
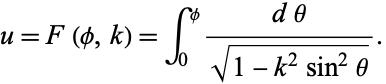(1)
|
The elliptic integral of the first kind is implemented in the Wolfram Language as EllipticF[phi, m] (note the use of the parameter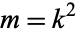 
instead of the modulus 
).
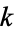Letting
Equation (1) can be written as
Letting
then the integral can also be written as
 |
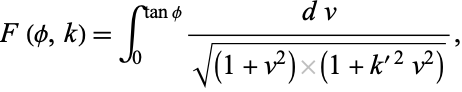(9)
|
where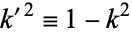 
is the complementary elliptic modulus.
The inverse function of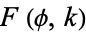 
is given by the Jacobi amplitude
 |
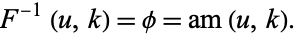(10)
|
The integral
 |
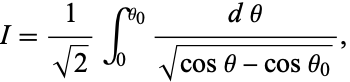(11)
|
which arises in computing the period of a pendulum, is also an elliptic integral of the first kind. Use
to write
so
 |
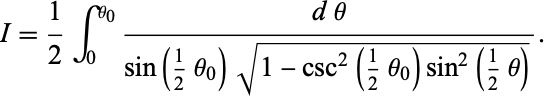(17)
|
Now let
 |
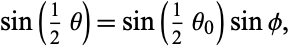(18)
|
so the angle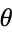 
is transformed to
 |
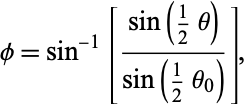(19)
|
which ranges from 0 to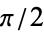 
as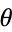 
varies from 0 to 
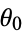. Taking the differential gives
 |
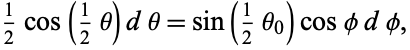(20)
|
or
 |
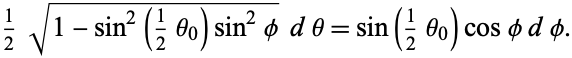(21)
|
Plugging this in gives
so
Making the slightly different substitution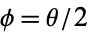 
, so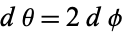 
leads to an equivalent, but more complicated expression involving an incomplete elliptic integral of the first kind,
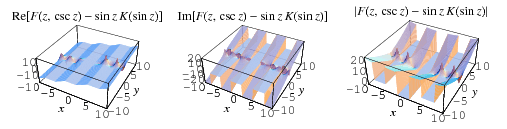
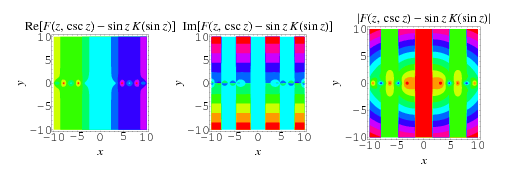
Therefore, the identity
 |
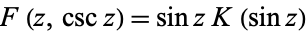(29)
|
holds over at least some region of the complex plane. The region of applicability is ![-pi/2<R[z]<pi/2](http://mathworld.wolfram.com/images/equations/EllipticIntegraloftheFirstKind/Inline72.gif)
, which is shown above.
The elliptic integral of the first kind satisfies
 |
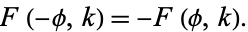(30)
|
Special values of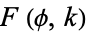 
include
where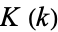 
is known as the complete elliptic integral of the first kind.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Elliptic Integrals." Ch. 17 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 587-607, 1972.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Spanier, J. and Oldham, K. B. "The Complete Elliptic Integrals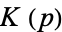 
and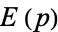 
" and "The Incomplete Elliptic Integrals 
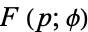and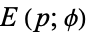 
." Chs. 61-62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987.
Tölke, F. "Parameterfunktionen." Ch. 3 in Praktische Funktionenlehre, zweiter Band: Theta-Funktionen und spezielle Weierstraßsche Funktionen. Berlin: Springer-Verlag, pp. 83-115, 1966.
Tölke, F. "Umkehrfunktionen der Jacobischen elliptischen Funktionen und elliptische Normalintegrale erster Gattung. Elliptische Amplitudenfunktionen sowie Legendresche F- und E-Funktion. Elliptische Normalintegrale zweiter Gattung. Jacobische Zeta- und Heumansche Lambda-Funktionen," and "Normalintegrale dritter Gattung. Legendresche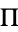 
-Funktion. Zurückführung des allgemeinen elliptischen Integrals auf Normalintegrale erster, zweiter, und dritter Gattung." Chs. 6-7 in Praktische Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen. Berlin: Springer-Verlag, pp. 58-144, 1967.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 122, 1997.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
