Lambda Function
المؤلف:
Gradshteyn, I. S. and Ryzhik, I. M
المصدر:
"The Functions nu(x), nu(x,a), mu(x,beta), mu(x,beta,alpha), lambda(x,y)." §9.64 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press
الجزء والصفحة:
...
25-3-2019
2999
Lambda Function
There are a number of functions in mathematics commonly denoted with a Greek letter lambda. Examples of one-variable functions denoted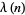 
with a lower case lambda include the Carmichael functions, Dirichlet lambda function, elliptic lambda function, and Liouville function. Examples of one-variable functions denoted 
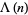with an upper case lambda 
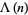include the Mangoldt function and the lambda function defined by Jahnke and Emden (1945).
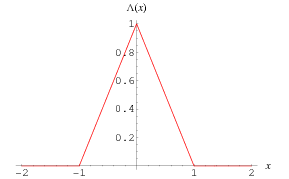
The triangle function, illustrated above, is commonly denoted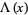 
.
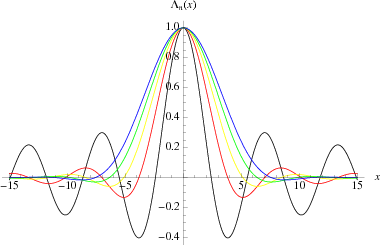
The lambda function defined by Jahnke and Emden (1945) is
 |
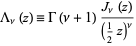(1)
|
where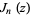 
is a Bessel function of the first kind and 
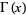is the gamma function. 
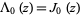, and taking 
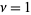gives the special case
 |
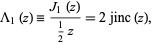(2)
|
where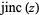 
is the jinc function.
A two-variable lambda function is defined as
 |
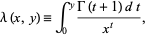(3)
|
where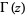 
is the gamma function (McLachlan et al. 1950, p. 9; Prudnikov et al. 1990, p. 798; Gradshteyn and Ryzhik 2000, p. 1109).
REFERENCES:
Gradshteyn, I. S. and Ryzhik, I. M. "The Functions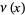 
, 
, 
, 
, 
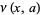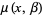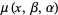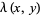." §9.64 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 1109, 2000.
Jahnke, E. and Emde, F. Tables of Functions with Formulae and Curves, 4th ed. New York: Dover, 1945.
McLachlan, N. W. et al. Supplément au formulaire pour le calcul symbolique. Paris: L'Acad. des Sciences de Paris, Fasc. 113, p. 9, 1950.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, 1990.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
