Content
المؤلف:
Séroul, R
المصدر:
Programming for Mathematicians. Berlin: Springer-Verlag
الجزء والصفحة:
p. 287
19-1-2019
1045
Content
There are several meanings of the word content in mathematics.
The content of a polytope or other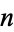 
-dimensional object is its generalized volume (i.e., its "hypervolume"). Just as a three-dimensional object has volume, surface area, and generalized diameter, an 
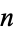-dimensional object has "measures" of order 1, 2, ..., 
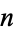. The content of a region can be computed in the Wolfram Language using RegionMeasure[reg].
The content of an integer polynomial ![P in Z[x]](http://mathworld.wolfram.com/images/equations/Content/Inline4.gif)
, denoted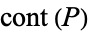 
, is the largest integer 
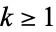such that 
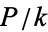also has integer coefficients. Gauss's lemma for contents states that if 
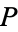and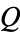 
are two polynomials with integer coefficients, then 
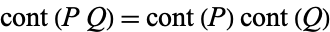(Séroul 2000, p. 287).
For a general univariate polynomial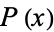 
, the Wolfram Language command FactorTermsList[poly, x] returns a list of three elements, the first being the integer content 
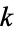, the second being the polynomial content, i.e., a primitive (with respect to all variables) polynomial that does not depend on 
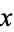and which divides all coefficients of 
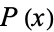, and the third element being the primitive part of 
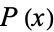. The original polynomial 
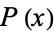is then the product of these three parts. For example, FactorTermsList[9E x^3+3E, x] returns ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/Content/Inline17.gif" style="height:14px; width:5px" />3, E, 1+3x^2![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/Content/Inline18.gif" style="height:14px; width:5px" />.
REFERENCES:
Séroul, R. Programming for Mathematicians. Berlin: Springer-Verlag, p. 287, 2000.
الاكثر قراءة في مواضيع عامة في الجبر
اخر الاخبار
اخبار العتبة العباسية المقدسة
