Linear Fractional Transformation
المؤلف:
Anderson, J. W
المصدر:
The Group of Möbius Transformations." §2.1 in Hyperbolic Geometry. New York: Springer-Verlag
الجزء والصفحة:
...
1-11-2018
824
Linear Fractional Transformation
A transformation of the form
 |
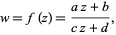(1)
|
where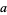 
, 
, 
, 
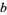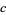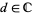and
 |
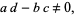(2)
|
is a conformal mapping called a linear fractional transformation. The transformation can be extended to the entire extended complex plane ![C^*=C union <span style=]()
{infty}" src="http://mathworld.wolfram.com/images/equations/LinearFractionalTransformation/Inline5.gif" style="height:14px; width:81px" /> by defining
(Apostol 1997, p. 26). The linear fractional transformation is linear in both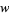 
and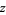 
, and analytic everywhere except for a simple pole at 
.
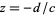Kleinian groups are the most general case of discrete groups of linear fractional transformations in the complex plane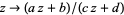 
.
Every linear fractional transformation except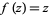 
has one or two fixed points. The linear fractional transformation sends circles and lines to circles or lines. Linear fractional transformations preserve symmetry. The cross ratio is invariant under a linear fractional transformation. A linear fractional transformation is a composition of translations, rotations, magnifications, and inversions.
To determine a particular linear fractional transformation, specify the map of three points which preserve orientation. A particular linear fractional transformation is then uniquely determined. To determine a general linear fractional transformation, pick two symmetric points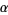 
and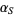 
. Define 
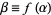, restricting 
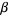as required. Compute 
. 
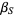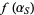then equals 
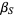since the linear fractional transformation preserves symmetry (the symmetry principle). Plug in 
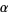and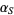 
into the general linear fractional transformation and set equal to 
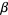and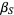 
. Without loss of generality, let 
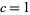and solve for 
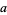and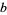 
in terms of 
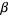. Plug back into the general expression to obtain a linear fractional transformation.
REFERENCES:
Anderson, J. W. "The Group of Möbius Transformations." §2.1 in Hyperbolic Geometry. New York: Springer-Verlag, pp. 19-25, 1999.
Apostol, T. M. "Möbius Transformations." Ch. 2.1 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 26-28, 1997.
Krantz, S. G. "Linear Fractional Transformations." §6.3 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 81-86, 1999.
Mathews, J. "The Moebius Transformation." http://www.ecs.fullerton.edu/~mathews/fofz/mobius/.
Needham, T. "Möbius Transformations and Inversion." Ch. 3 in Visual Complex Analysis. New York: Clarendon Press, pp. 122-188, 2000.
الاكثر قراءة في التحليل العقدي
اخر الاخبار
اخبار العتبة العباسية المقدسة
