Maximum
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
23-8-2018
2650
Maximum
The largest value of a set, function, etc. The maximum value of a set of elements ![A=<span style=]()
{a_i}_(i=1)^N" src="http://mathworld.wolfram.com/images/equations/Maximum/Inline1.gif" style="height:19px; width:64px" /> is denoted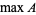 
or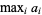 
, and is equal to the last element of a sorted (i.e., ordered) version of 
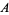. For example, given the set ![<span style=]()
{3,5,4,1}" src="http://mathworld.wolfram.com/images/equations/Maximum/Inline5.gif" style="height:14px; width:62px" />, the sorted version is ![<span style=]()
{1,3,4,5}" src="http://mathworld.wolfram.com/images/equations/Maximum/Inline6.gif" style="height:14px; width:62px" />, so the maximum is 5. The maximum and minimum are the simplest order statistics.
The maximum value of a variable 
is commonly denoted 
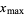(Strang 1988, pp. 286-287 and 301-303) or 
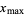(Golub and Van Loan 1996, p. 74). In this work, the convention 
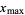is used.
The maximum of a set of elements is implemented in the Wolfram Language as Max[list] and satisfies the identities
Definite integrals include
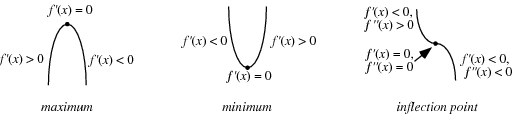
A continuous function may assume a maximum at a single point or may have maxima at a number of points. A global maximum of a function is the largest value in the entire range of the function, and a local maximum is the largest value in some local neighborhood.
For a function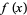 
which is continuous at a point 
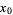, a necessary but not sufficient condition for 
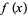to have a local maximum at 
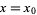is that 
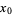be a critical point (i.e., 
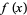is either not differentiable at 
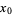or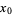 
is a stationary point, in which case 
).
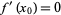The first derivative test can be applied to continuous functions to distinguish maxima from minima. For twice differentiable functions of one variable,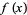 
, or of two variables, 
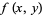, the second derivative test can sometimes also identify the nature of an extremum. For a function 
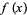, the extremum test succeeds under more general conditions than the second derivative test.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.
Golub, G. and Van Loan, C. Matrix Computations, 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.
Niven, I. Maxima and Minima without Calculus. Washington, DC: Math. Assoc. Amer., 1982.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Minimization or Maximization of Functions." Ch. 10 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 387-448, 1992.
Strang, G. Linear Algebra and its Applications, 3rd ed. Philadelphia, PA: Saunders, 1988.
Tikhomirov, V. M. Stories About Maxima and Minima. Providence, RI: Amer. Math. Soc., 1991.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
