Laplace,s Equation--Spherical Coordinates
المؤلف:
Morse, P. M. and Feshbach, H
المصدر:
Methods of Theoretical Physics, Part I. New York: McGraw-Hill
الجزء والصفحة:
...
21-7-2018
2729
Laplace's Equation--Spherical Coordinates
In spherical coordinates, the scale factors are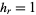 
, 
, 
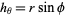, and the separation functions are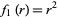 
, 
, 
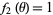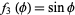, giving a Stäckel determinant of 
.
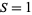The Laplacian is
 |
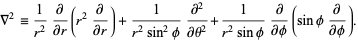(1)
|
To solve Laplace's equation in spherical coordinates, attempt separation of variables by writing
 |
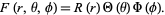(2)
|
Then the Helmholtz differential equation becomes
 |
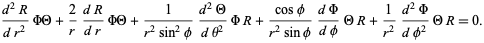(3)
|
Now divide by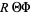 
,
 |
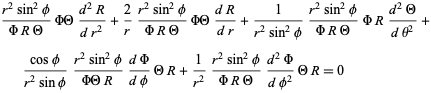(4)
|
 |
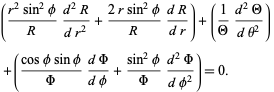(5)
|
The solution to the second part of (5) must be sinusoidal, so the differential equation is
 |
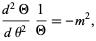(6)
|
which has solutions which may be defined either as a complex function with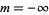 
, ..., 
 |
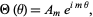(7)
|
or as a sum of real sine and cosine functions with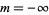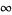 
, ..., 
 |
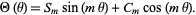(8)
|
Plugging (6) back into (7),
 |
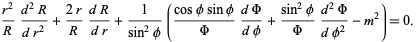(9)
|
The radial part must be equal to a constant
 |
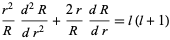(10)
|
 |
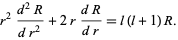(11)
|
But this is the Euler differential equation, so we try a series solution of the form
 |
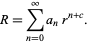(12)
|
Then
 |
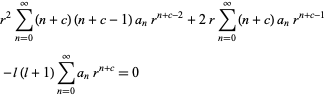(13)
|
 |
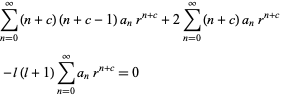(14)
|
 |
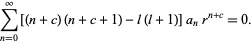(15)
|
This must hold true for all powers of 
. For the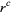 
term (with 
),
 |
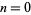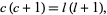(16)
|
which is true only if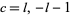 
and all other terms vanish. So 
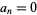for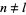 
, 
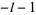. Therefore, the solution of the 
component is given by
 |
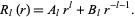(17)
|
Plugging (17) back into (◇),
 |
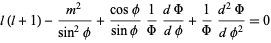(18)
|
 |
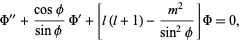(19)
|
which is the associated Legendre differential equation for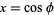 
and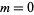 
, ..., 
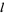. The general complex solution is therefore
 |
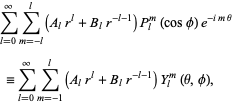(20)
|
where
 |
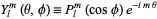(21)
|
are the (complex) spherical harmonics. The general real solution is
 |
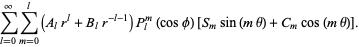(22)
|
Some of the normalization constants of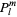 
can be absorbed by 
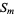and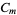 
, so this equation may appear in the form
 |
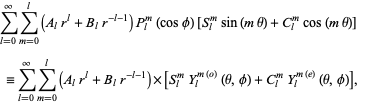(23)
|
where
 |
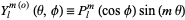(24)
|
 |
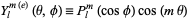(25)
|
are the even and odd (real) spherical harmonics. If azimuthal symmetry is present, then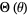 
is constant and the solution of the 
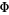component is a Legendre polynomial 
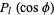. The general solution is then
 |
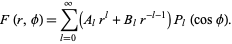(26)
|
REFERENCES:
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, p. 244, 1959.
Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, p. 27, 1988.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 514 and 658, 1953.
الاكثر قراءة في المعادلات التفاضلية الجزئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
