Helmholtz Differential Equation--Elliptic Cylindrical Coordinates
المؤلف:
Abramowitz, M. and Stegun, I. A
المصدر:
"Mathieu Functions." Ch. 20 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
18-7-2018
1580
Helmholtz Differential Equation--Elliptic Cylindrical Coordinates
In elliptic cylindrical coordinates, the scale factors are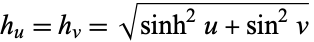 
, 
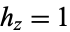, and the separation functions are 
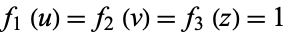, giving a Stäckel determinant of 
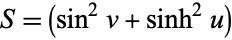. The Helmholtz differential equation is
 |
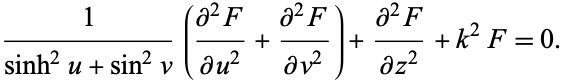(1)
|
Attempt separation of variables by writing
 |
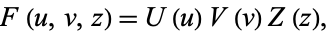(2)
|
then the Helmholtz differential equation becomes
 |
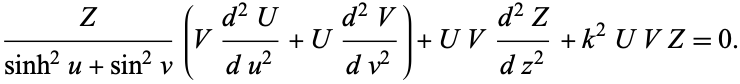(3)
|
Now divide by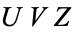 
to give
 |
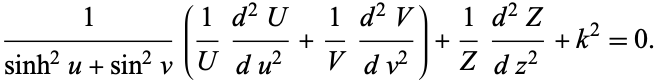(4)
|
Separating the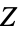 
part,
 |
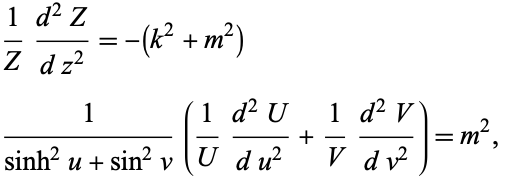(5)
|
so
 |
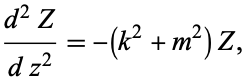(6)
|
which has the solution
 |
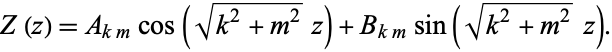(7)
|
Rewriting (◇) gives
 |
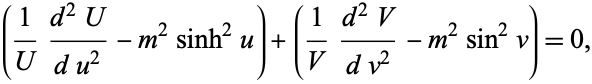(8)
|
which can be separated into
so
 |
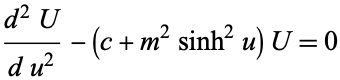(11)
|
 |
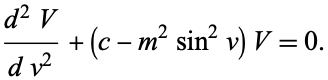(12)
|
Now use
![sinh^2u=1/2[cosh(2u)-1]](http://mathworld.wolfram.com/images/equations/HelmholtzDifferentialEquationEllipticCylindricalCoordinates/NumberedEquation11.gif) |
(13)
|
![sin^2v=1/2[1-cos(2v)]](http://mathworld.wolfram.com/images/equations/HelmholtzDifferentialEquationEllipticCylindricalCoordinates/NumberedEquation12.gif) |
(14)
|
to obtain
![(d^2U)/(du^2)-<span style=]() {c+1/2m^2[cosh(2u)-1]}U=0 " class="numberedequation" src="http://mathworld.wolfram.com/images/equations/HelmholtzDifferentialEquationEllipticCylindricalCoordinates/NumberedEquation13.gif" style="border:0px; height:40px; width:233px" /> |
(15)
|
![(d^2V)/(dv^2)+<span style=]() {c-1/2m^2[1-cos(2v)]}V=0. " class="numberedequation" src="http://mathworld.wolfram.com/images/equations/HelmholtzDifferentialEquationEllipticCylindricalCoordinates/NumberedEquation14.gif" style="border:0px; height:40px; width:227px" /> |
(16)
|
Regrouping gives
![(d^2U)/(du^2)-[(c-1/2m^2)+1/2m^2cosh(2u)]U=0](http://mathworld.wolfram.com/images/equations/HelmholtzDifferentialEquationEllipticCylindricalCoordinates/NumberedEquation15.gif) |
(17)
|
![(d^2V)/(dv^2)+[(c-1/2m^2)+1/2m^2cos(2v)]V=0.](http://mathworld.wolfram.com/images/equations/HelmholtzDifferentialEquationEllipticCylindricalCoordinates/NumberedEquation16.gif) |
(18)
|
Let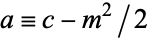 
and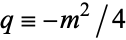 
, then these become
![(d^2V)/(dv^2)+[a-2qcos(2v)]V=0](http://mathworld.wolfram.com/images/equations/HelmholtzDifferentialEquationEllipticCylindricalCoordinates/NumberedEquation17.gif) |
(19)
|
![(d^2U)/(du^2)-[a-2qcosh(2u)]U=0.](http://mathworld.wolfram.com/images/equations/HelmholtzDifferentialEquationEllipticCylindricalCoordinates/NumberedEquation18.gif) |
(20)
|
Here, (19) is the mathieu differential equation and (20) is the modified mathieu differential equation. These solutions are known as mathieu functions.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Mathieu Functions." Ch. 20 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 721-746, 1972.
Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed.New York: Springer-Verlag, pp. 17-19, 1988.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 514 and 657, 1953.
الاكثر قراءة في المعادلات التفاضلية الجزئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
