Green,s Function--Helmholtz Differential Equation
المؤلف:
Arfken, G
المصدر:
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
الجزء والصفحة:
...
22-5-2018
1599
Green's Function--Helmholtz Differential Equation
The inhomogeneous Helmholtz differential equation is
 |
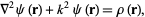(1)
|
where the Helmholtz operator is defined as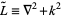 
. The Green's function is then defined by
 |
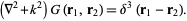(2)
|
Define the basis functions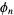 
as the solutions to the homogeneous Helmholtz differential equation
 |
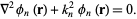(3)
|
The Green's function can then be expanded in terms of the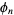 
s,
 |
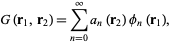(4)
|
and the delta function as
 |
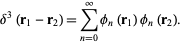(5)
|
Plugging (◇) and (◇) into (◇) gives
![del ^2[sum_(n=0)^inftya_n(r_2)phi_n(r_1)]+k^2sum_(n=0)^inftya_n(r_2)phi_n(r_1)=sum_(n=0)^inftyphi_n(r_1)phi_n(r_2).](http://mathworld.wolfram.com/images/equations/GreensFunctionHelmholtzDifferentialEquation/NumberedEquation6.gif) |
(6)
|
Using (◇) gives
 |
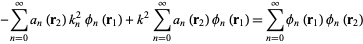(7)
|
 |
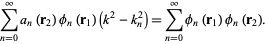(8)
|
This equation must hold true for each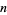 
, so
 |
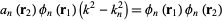(9)
|
 |
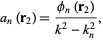(10)
|
and (◇) can be written
 |
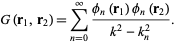(11)
|
The general solution to (◇) is therefore
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 529-530, 1985.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
