
Vector Derivative
 المؤلف:
Gradshteyn, I. S. and Ryzhik, I. M
المؤلف:
Gradshteyn, I. S. and Ryzhik, I. M
 المصدر:
"Vector Field Theorem." Ch. 10 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press
المصدر:
"Vector Field Theorem." Ch. 10 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press
 الجزء والصفحة:
...
الجزء والصفحة:
...
 19-5-2018
19-5-2018
 2313
2313
Vector Derivative
A vector derivative is a derivative taken with respect to a vector field. Vector derivatives are extremely important in physics, where they arise throughout fluid mechanics, electricity and magnetism, elasticity, and many other areas of theoretical and applied physics.
The following table summarizes the names and notations for various vector derivatives.
| symbol |
vector derivative |
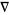 |
gradient |
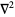 |
Laplacian or vector Laplacian |
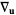 or or 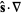 |
directional derivative |
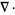 |
divergence |
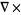 |
curl |
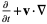 |
convective derivative |
Vector derivatives can be combined in different ways, producing sets of identities that are also very important in physics.
Vector derivative identities involving the curl include
In Cartesian coordinates
In spherical coordinates,
Vector derivative identities involving the divergence include
In Cartesian coordinates,
In spherical coordinates,
By symmetry,
Vector derivative identities involving the gradient include
Vector second derivative identities include
This very important second derivative is known as the Laplacian.
Identities involving combinations of vector derivatives include
where (64) and (65) follow from divergence rule (2).
REFERENCES:
Gradshteyn, I. S. and Ryzhik, I. M. "Vector Field Theorem." Ch. 10 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, pp. 1081-1092, 2000.
Morse, P. M. and Feshbach, H. "The Differential Operator 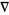 " and "Table of Useful Vector and Dyadic Equations." In Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 31-44, 50-54, and 114-115, 1953.
" and "Table of Useful Vector and Dyadic Equations." In Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 31-44, 50-54, and 114-115, 1953.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


