


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 18-8-2016
Date: 9-8-2016
Date: 29-8-2016
|
Wave Attenuation
Consider a medium with nonzero conductivity σ(J = σE gives the current density) and no net charge (ρ = 0).
a) Write the set of Maxwell’s equations appropriate for this medium.
b) Derive the wave equation for E ( or B) in this medium,
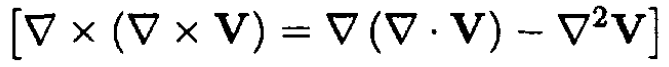
c) Consider a monochromatic wave moving in the +x direction with Ey (or Ez or By or Bz ) given by

Show that this wave has an amplitude which decreases exponentially; find the attenuation length (skin depth).
d) For sea water (σ ≈ 5mho/m, or 4.5 × 1010s-1 in cgs units), and using radio waves of long wavelength ω = 5 × 105s-1, calculate the attenuation length. (Why is it hard to communicate with submerged submarines?) You can take for sea water ε = 1, μ = 1.
SOLUTION
a, b) We obtain the equation for the electric (magnetic) field in the same way as
 (1)
(1)
c) Now, taking Ey in the form Ey = ѱ0ei(kx – ωt) and substituting into (1) yields
 (2)
(2)
We have
 (3)
(3)
To solve for the square root of the complex expression in (3), write
 (4)
(4)
where a and are real, and

By squaring (S.3.47.4), we find
 (5)
(5)
 (6)
(6)
Taking a from (S.3.47.6) and substituting it into (S.3.47.5), we have for b

where we have chosen the branch of the root with the plus sign to satisfy σ = 0 (vacuum) b = k'' = 0 (no dissipation). So
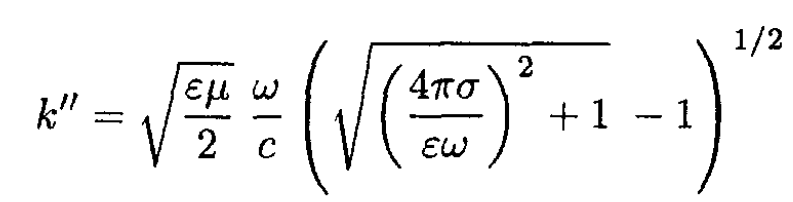 (7)
(7)
Therefore, the attenuation length (1/e point) for the amplitude
 (8)
(8)
whereas for the intensity, the attenuation length is δ/2.
d) For the frequency given in the problem,
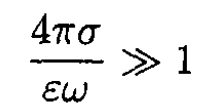
and so we can disregard the 1’s in (8) and rewrite it as

At a depth of 10 m below the surface, the intensity attenuation at this frequency will be

which implies that transmission of signals to submerged submarines will require much lower frequencies, f ≤ 10 – 102 Hz.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة لجامعة سومر للمشاركة في حفل التخرج المركزي الخامس
|
|
|