


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 30-8-2016
Date: 6-9-2016
Date: 30-8-2016
|
Elastic Collision and Rotation Angle
Consider an elastic collision (namely a collision where the particles involved do not change their internal state) of an incident particle of mass m1, momentum p1, and energy ε1 (see notation below), with a particle of mass m2 at rest. Let the final energies be ἓ1 and ἓ2 and the final momenta be  and
and 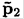 (all of this in the laboratory frame).
(all of this in the laboratory frame).
a) In the center of mass frame (CMF), denote by p10 and p20 the incoming momenta of the two particles and by ε10, ε20 their energies.
One has
 (i)
(i)
where p0 is a vector. In the center of mass frame the collision rotates the direction of the momenta. Let the outgoing momenta and energies be  and the rotation angle be χ. From conservation of energy and momentum, what can you tell about
and the rotation angle be χ. From conservation of energy and momentum, what can you tell about  About ἓ10 and ἓ20?
About ἓ10 and ἓ20?
b) From the energy and momentum conservation laws,
 (ii)
(ii)
show that
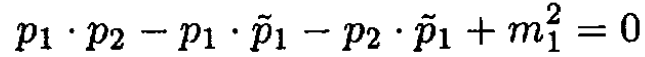 (iii)
(iii)
c) Evaluate the first and third terms of the left-hand side of equation (3) in the laboratory frame. Evaluate the second term in the CMF in terms of p0 and χ (and masses). Now use equation (3) to find an expression for (ἓ - ε) in terms of p0 and χ (and masses).
d) Find an expression for p0 in terms of ε1 (and masses) by evaluating p1 . p2 both in the laboratory and CMF.
e) Give ἓ1 and ἓ2 in terms of ε1, ε2, and χ.
f) Consider the case for maximal energy transfer. What is the value of χ? For this case find the ratio of the final kinetic energy to the incident kinetic energy for the incoming particle (in the laboratory frame).
Notation: Here we use

SOLUTION
a) Express conservation of energy as
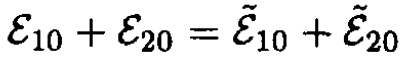 (1)
(1)
Conservation of momentum gives
 (2)
(2)
From the information given and (2)
 (3)
(3)
These equations may be rearranged to yield
 (4)
(4)
Substituting (1) into (4) yields
 (5)
(5)
Adding or subtracting (1) from (5) results in
 (6)
(6)
and by (3),
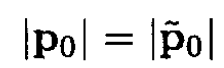 (7)
(7)
b) Inspection of (iii) seems to indicate the way to proceed, since  does not appear. Subtract
does not appear. Subtract 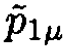 from both sides of (ii) and square:
from both sides of (ii) and square:
 (8)
(8)
c) The instructions in (c) exploit the invariance of a product of 4-vectors under a Lorentz transformation, here from the laboratory frame to the CMF. In the laboratory frame

So we have
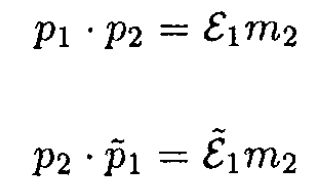
In the CMF

where

Substitution into (8) yields

Now, ε210 = p20 + m21, so
 (9)
(9)
d) From (c), p1 . p2 in the laboratory frame equals ε1m2, and p1 . p2 in the CMF equals ε10ε20 + p20, so
 (10)
(10)
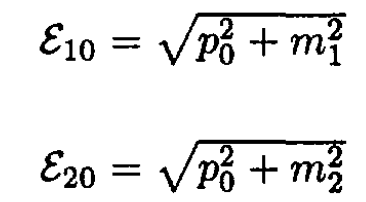
Rearrange and square (10):
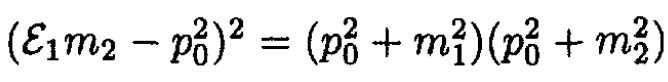 (11)
(11)
yielding
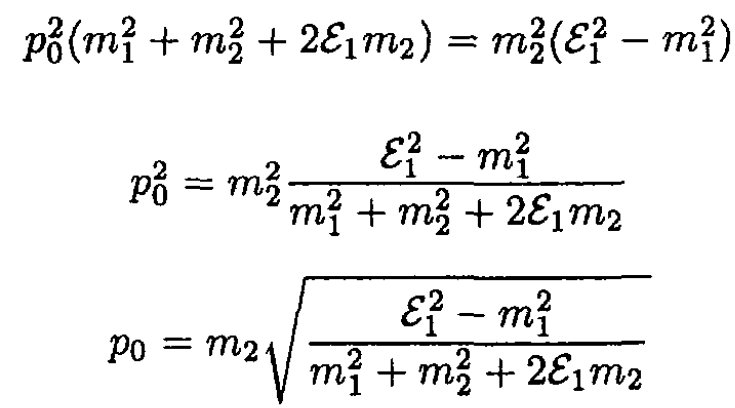 (12)
(12)
If the incident mass has no kinetic energy, in the CMF it should have no momentum, as seen in (12). If m2/m1 → 0, then the frame of particle 1 is the CMF, so p0 again should equal 0.
e) From (9) and (12) we have

Conservation of energy gives
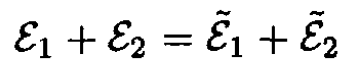
So

f) We maximize 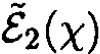 by letting χ = π. So
by letting χ = π. So

For m1 = m2, the final kinetic energy of the incident particle equals 0.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|