


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 24-7-2016
التاريخ: 25-4-2016
التاريخ: 2024-02-27
التاريخ: 21-4-2016
|
القوة المؤثرة على شحنة متحركة
بعد ان نتوصل الى كيفية حساب شدة المجال الكهربائي في أية نقطة قريبة من شحنة نقطية في حالة حركة بسرعة ثابتة من الممكن الآن استنتاج القوة التي تتعرض لها شحنة نقطية ساكنة في مجال شحنة نقطية اخرى متحركة.
ومن الممكن ان نأخذ الحالة التي تكون فيها الشحنة متحركة في مجال شحنات ساكنة. وقد تكون هذه الشحنة الكترونا يتحرك بين لوحين مشحونين أو جسميا مشحونا يتحرك ضمن مجال كولوم الذي يحيط بنواة ذرة ما. وهنا نلاحظ ان مصادر المجال كلها ساكنة في محاور اسناد معينة مثل المحاور المختبرية. ان القوة المؤثرة على هذه الشحنة تساوي معدل التغير الذي يحصل في الزخم.
ولحساب هذه القوة نعتبر محور الاسناد sʹ الذي يتحرك بسرعة مساوية لسرعة الجسيم. اذن اي مشاهد في هذا المحور يرى ان الجسيم المشحون في حالة سكون. اما الشحنات الاخرى فتشاهد تتحرك بالاتجاه المعاكس بسرعة مساوية بالمقدار لسرعة الجسيم التي تساوي v. لذا فان القوة المؤثرة على الشحنة الساكنة q تكون مساوية الى qEʹ حيث ان Eʹ شدة المجال الكهربائي عند موقع الشحنة في محور الاسناد sʹ ولتوضيح ذلك نفرض ما يلي :
اذا كانت شحنة الاختبار في حالة حركة فان قوتين تؤثران عليها، احداهما كهربائية والاخرى مغناطيسية.

الشكل (1.1) : (a) شحنة المصدر Q في حالة حركة باتجاه الاحداثي x. وشحنة الاختبار q تتحرك ضمن مجال Q بسرعة u في زمن t =0. (b) عندما ينقل الحدث الى محور اسناد آخر تصبح شحنة المصدر ساكنة وفي هذه الحالة يمكن تطبيق قانون كولوم.
ولكي ندرس هذه الحالة بصورة أوضح وابسط ننقل الحدث الى محور الاسناد sʹ الذي يتحرك بسرعة ثابتة v باتجاه الاحداثي x كما موضح في الشكل (1.1b) وفي هذا المحور يشاهد ان شحنة المصدر في حالة سكون وشحنة الاختبار تغيرت سرعتها الى  بالاتجاه الموضح في شكل. وبما ان الشحنة Q ساكنة فان القوة المؤثرة على شحنة الاختبار q هي قوة كهربائية فقط. اذن قانون كولوم يمكن تطبيقه في هذه الحالات لحساب القوة التي تؤثر على تلك الشحنة في ذلك الموقع. من معادلات تحويل القوة نكتب :
بالاتجاه الموضح في شكل. وبما ان الشحنة Q ساكنة فان القوة المؤثرة على شحنة الاختبار q هي قوة كهربائية فقط. اذن قانون كولوم يمكن تطبيقه في هذه الحالات لحساب القوة التي تؤثر على تلك الشحنة في ذلك الموقع. من معادلات تحويل القوة نكتب :
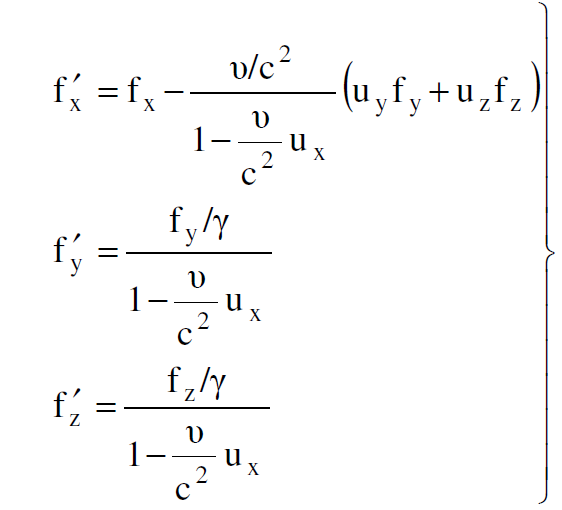 (1.1)
(1.1)
لندرس الان هاتين الحالتين :
اولا – شحنة الاختبار تشاهد في محور الاسناد s في حالة سكون أي ان 0=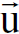 .
.
ثانيا – شحنة الاختبار تشاهد في حالة حركة بسرعة y =
= في زمن t=0 في محور الاسناد نفسه وفي الموقع (x, y, 0).
في زمن t=0 في محور الاسناد نفسه وفي الموقع (x, y, 0).
بالنسبة للحالة الاولى تختزل المعادلات (1.1) الى الصيغة الاتية :
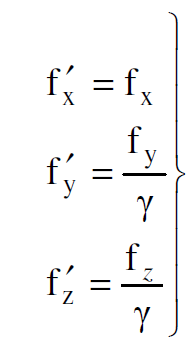 (1.2)
(1.2)
من قانون نيوتن الثاني ان معدل التغير الذي يحصل للزخم بالنسبة للزمن يساوي القوة المؤثرة على الجسيم. نكتب اذن المعادلات (1.2) بالشكل :
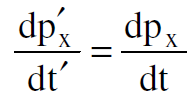 (1.3)
(1.3)
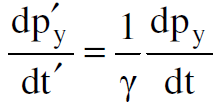 (1.4)
(1.4)
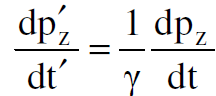 (1.5)
(1.5)
وبما ان الزخمين y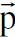 , z
, z عموديان على اتجاه الحركة لشحنة المصدر فيمكن جمعهما بزخم واحد هو ┴
عموديان على اتجاه الحركة لشحنة المصدر فيمكن جمعهما بزخم واحد هو ┴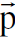 اما الزخم x
اما الزخم x فهو باتجاه حركة الشحنة ويكتب بالصيغة II
فهو باتجاه حركة الشحنة ويكتب بالصيغة II وهكذا تختزل المعادلات الثلاثة الاخيرة الى معادلتين وتكتب كالآتي :
وهكذا تختزل المعادلات الثلاثة الاخيرة الى معادلتين وتكتب كالآتي :
 (1.6)
(1.6)
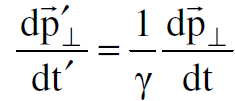 (1.7)
(1.7)
وطبقا للعلاقتين

نحصل على :
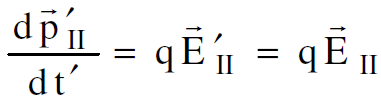
 (1.8)
(1.8)
وكذلك :
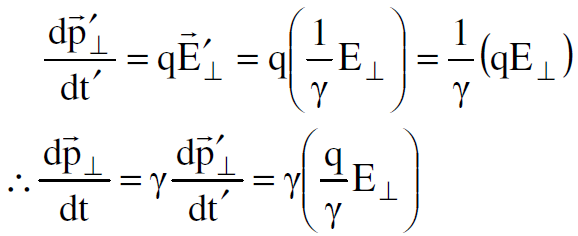
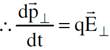 (1.9)
(1.9)
نستنتج مما تقدم من العلاقتين (1.8)، (1.9) أن القوة الكهربائية المؤثرة على جسيم مشحون في حالة سكون في محور الاسناد s تنتشر فيه خطوط قوى كهربائية ومغناطيسية ناتجة من الشحنة المتحركة بالقرب من ذلك الجسيم تساوي حاصل ضرب مقدار الشحنة التي يحملها ذلك الجسيم في شدة المجال الكهربائي عند موقع الجسيم. ولتوضيح الحالة الثانية نعتبر الشكل (1.2) ونستخدم معادلات تحويل القوة من محور الاسناد .. الى s وكذلك معادلات تحويل السرعة من s الى sʹ فيكون:
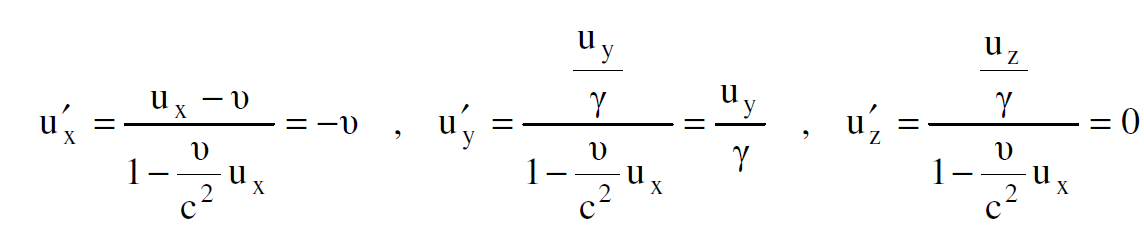

الشكل (1.2) : شحنة المصدر في حالة حركة في s. وشحنة الاختبار في حالة حركة بسرعة u باتجاه الاحداثي y. وبنقل الحدث الى sʹ تصبح شحنة المصدر في حالة سكون وبهذا يمكن تطبيق قانون كولوم.
اما بالنسبة للقوة فنحسب اولا مركبات القوة المؤثرة على الجسيم في محور الاسناد sʹ فنجد :

تكتب الان معادلات تحويل القوة بالصورة :
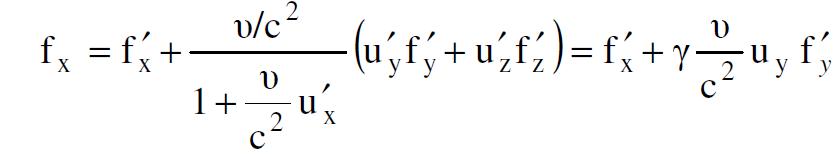
ومن تحويلات لورنس في زمن t = 0 ينتج ان :
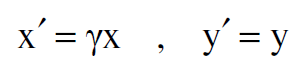
وهكذا تكتب المعادلة الاخيرة بالصورة :
 (1.10)
(1.10)
اما مركبة القوة باتجاه المحور y فهي :
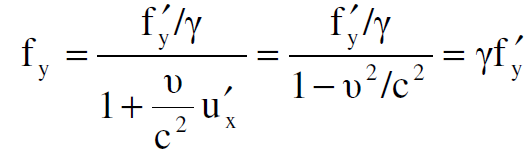
 (1.11)
(1.11)
وكذلك

اذن القوة المؤثرة على الجسيم المشحون في محور الاسناد s تعتمد على سرعة الجسيم اذا كان اتجاهها عموديا على حركة شحنة المصدر.
ولو فرضنا الان ان u= uy=0 (أي ان الشحنة في حالة سكون) فان :
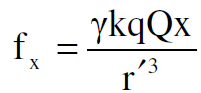
حيث ان :

اي ان الجسيم المشحون في هذه الحالة تؤثر عليه قوة تعتمد على سرعة شحنة المصدر فقط.
اذا نظرنا الان الى العلاقة (1.10) بإمعان نلاحظ ان القوة fx مكونة من جزئين هما :
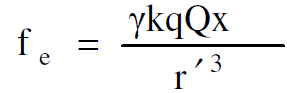 (1.12)
(1.12)
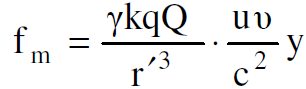 (1.13)
(1.13)
يلاحظ من الشكل (1.2) ان اتجاه المجال المغناطيسي 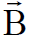 الذي تولده شحنة المصدر Q عند موقع شحنة الاختبار q هو باتجاه القارئ عمودي على الورقة. اذن القوة المغناطيسية تكون باتجاه الاحداثي x وتتناسب مع
الذي تولده شحنة المصدر Q عند موقع شحنة الاختبار q هو باتجاه القارئ عمودي على الورقة. اذن القوة المغناطيسية تكون باتجاه الاحداثي x وتتناسب مع 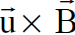 اي ان :
اي ان :
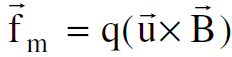 (1.14)
(1.14)
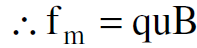
وبمقارنة المعادلتين (1.13)، (1.14) نستنتج ان :
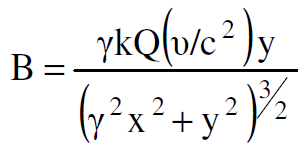 (1.14)
(1.14)
ومن العلاقتين (1.11)، (1.12) نلاحظ ان المجال الكهربائي المؤثر على شحنة الاختبار يساوي :

حيث ان : 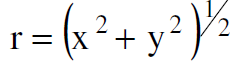
يلاحظ الان من الشكل (1.2) أن 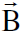 باتجاه z و
باتجاه z و  باتجاه
باتجاه 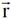 عند موقع شحنة الاختبار q. لذا يكتب متجه كثافة الفيض المغناطيسي وشدة المجال الكهربائي بالصورة :
عند موقع شحنة الاختبار q. لذا يكتب متجه كثافة الفيض المغناطيسي وشدة المجال الكهربائي بالصورة :

اذ ان 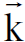 وحدة المتجه باتجاه الاحداثي z وأن
وحدة المتجه باتجاه الاحداثي z وأن  متجه الموضع للشحنة Q. ولو دققنا النظر في المعادلة الاخيرة لكثافة الفيض المغناطيسي نجد أن الطرف الايمن منها يتضمن المتجه
متجه الموضع للشحنة Q. ولو دققنا النظر في المعادلة الاخيرة لكثافة الفيض المغناطيسي نجد أن الطرف الايمن منها يتضمن المتجه 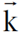 vy وهو مركبة المتجه
vy وهو مركبة المتجه  باتجاه z اي ان :
باتجاه z اي ان :
اما المركبتان الاخريان باتجاه x و y فكل منهما تساوي صفرًا ويتضح ذلك من مفكوك حاصل الضرب الاتجاهي 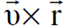 .
.
تكتب  مرة اخرى لتأخذ الصيغة :
مرة اخرى لتأخذ الصيغة :

وطبقا لهذه العلاقة الاخيرة متجه كثافة الفيض 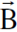 يكون عموديا على كل من
يكون عموديا على كل من 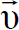 و
و 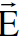 اي انه عمودي على المستوى الذي يضم الاحداثيين x وy.
اي انه عمودي على المستوى الذي يضم الاحداثيين x وy.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|