


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 22-1-2021
Date: 23-1-2021
Date: 2-2-2021
|
RATE EQUATION ANALYSIS FOR ATOMIC TRANSITIONS
We now take a more exhaustive approach to the analysis of laser rate equations based on the nature of the energy levels themselves. Before we examine laser systems, consider a simple atomic system involving only two energy levels, N1 and N2, where N1 is the lower level for the transition and N2 the upper level. An atom at the lower level can absorb a photon of a specific energy and be promoted to the upper level. Similarly, an atom at the upper level can jump to the lower level and in the process emit a photon of light with energy corresponding to the energy difference between the two levels. In addition to displaying the spontaneous emission of a photon, the same atom at the upper level can be stimulated to emit a photon of light in the process of stimulated emission.
We begin by defining the cross section of an atom, which specifies the effective size of an atom. The larger the atomic cross section, the larger the target to interact with other atoms or particles or an optical wave. In a physical sense, one would expect a real atom to have a cross section of only a few atomic radii in diameter. We find that Bohr postulated that the radius of an orbit was given by
r = n2a0
where n is the quantum number and a0 is the Bohr radius (5.29 × 10-11 m). Following this logic, for an atom with an n = 2 outer orbit, we expect the cross section to be only two 2 A ° (2 × 10-10 m) radius. The odds of such a small object interacting with anything would be slim (unless the pressures involved were extremely high, so as to increase the number of atoms available for interaction). In reality, though, atoms are found to have cross sections of 100 nm or more! The large
The electric dipole of the atom, which acts as a tiny antenna capturing signals. Cross section is important because it gives rise to a figure called the transitional probability. For a given transition between two energy levels, this figure represents the odds that a particular atom will make a particular transition and is denoted W. It has units of probability per atom per second (measured in units of s-1) and is a real physical value, which may be determined experimentally by examining the absorption of an atomic transition across the entire bandwidth of the transition to determine time constants (which also determine the Einstein A coefficient, important in rate equations). Experimental values may be referenced using a source of atomic data such as the CRC Handbook of Chemistry and Physics (Boca Raton, FL: CRC Press), a standard source for data such as these. The CRC Handbook lists transitional probabilities for various atomic and ionic species in units of 108 s-1 and gives statistical weight and upper energy levels allowing the calculation of atomic oscillator strength and transition strength, two useful figures when considering the usefulness of a particular transition for lasing action. Transition strength, denoted S, is simply the integral of cross section across all frequencies. It is related to the radiative lifetime and wavelength of the transition itself and may be calculated from those parameters.
As an example, consider the transitional probabilities of the red (632.82 nm) and green (543.37 nm) transitions of neon responsible for two popular lines of the helium–neon laser. The red line has a transitional probability listed as 0.0339 × 108 s-1, and the green line, as 0.00283 × 108 s-1. It is immediately apparent that the red transition (which shares exactly the same upper energy level as the green transition) is much more probable, so that if both transitions are allowed to oscillate (i.e., through the use of broadband mirrors in a laser cavity) the red transition will probably overtake the green. Conversion to line strength also reveals why the red transition is much more popular in the He Ne system.
Now that we have defined probability (and cross section), we can examine an atomic system by defining the rate of energy flow into or out of a particular level as the change in population of the level (ΔN) over a given time period (Δt). In proper calculus notation we express a rate as dN/dt, which has units of atoms per second. Simply put, the rate equation for any given level is
r = dN/dt = WN (1.1)
where W is the probability of a transition and N is the population of the level. For an atom at the lower energy level (N1) the probability of absorbing a photon and being promoted to the upper level is W12, where the subscripts indicate the transition and the direction in which it is occurring (in this case, from level 1 to level 2). In the case of the upper level, though, there are two probabilities: the probability of spontaneous emission occurring (related to the lifetime of the level) as well as the probability of stimulated emission occurring. We can define, then, these two probabilities as W21, the stimulated emission probability, and 1/τ21, the spontaneous emission probability (where τ21 is the spontaneous decay time for the upper level, which includes decay by radiative and non-radiative means. That this is the inverse of the Einstein A coefficient). Spontaneous emission does not depend on incident light but solely on population at an upper energy level available to make the downward transition. The situation in a two-level system is outlined in Figure 1.1.
It must be noted that W (the pumping transition probability measured in units of s-1) is a function of the intensity of incident light. For an absorption process it is obvious that more light intensity results in a higher probability of absorption of a photon. The same holds true for stimulated emissions, where a higher intensity of light results in a higher probability of a stimulated emission occurring. The probability of a single event (absorption or stimulated emission) occurring is related to the cross section (defined earlier) by
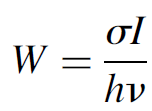 (1.2)
(1.2)
where σ is the cross section of the transition (in cm2), I the intensity of the incident photon stream (in W/cm2), and hv the energy of a single photon in the stream (in joules). The cross section of real gas atoms at low pressures (conditions normally encountered in gas lasers) usually fall in the range of 1 × 10-11 to 1 × 10-13 cm2. For example, the neon transition that produces the He Ne gas laser output at 632.8 nm has a cross section of 1 × 10-13 cm2.We may also relate this probability to the Einstein B coefficient, as
W12 = B12ρ (1.3)
where ρ is the energy density. Multiplying this probability parameter by the number of atoms at a specific level results in the rate at which atoms make the transition (in units of atoms per unit time). This relationship may be derived by combining equation (1.3). We now begin an analysis of a two-level system by expressing the rates at which atoms populate each level. In a two-level system we can express the rate of each
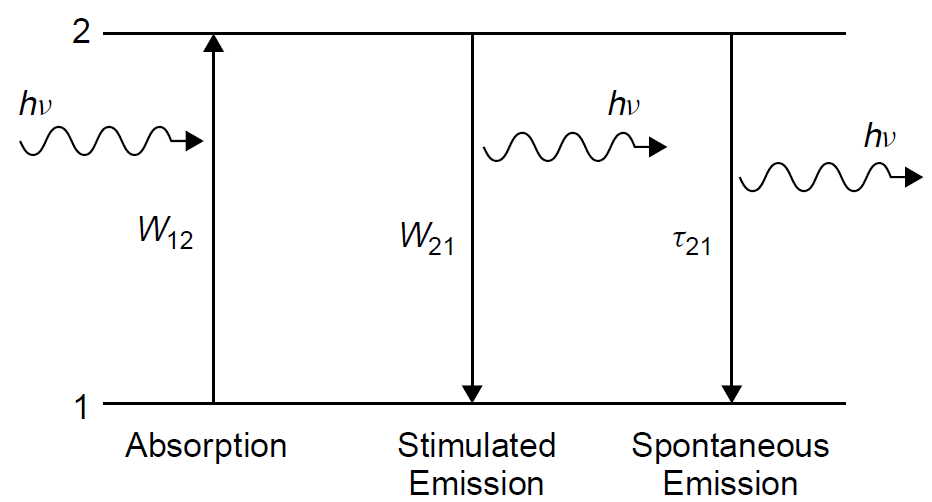
Figure 1.1. Processes in a two-level atomic system.
level by summing mechanisms that serve to add to the level and subtracting mechanisms that serve to depopulate the level as follows. For the upper level:
 (1.4)
(1.4)
Similarly, for the lower level:
 (1.5)
(1.5)
In these equations N1(t) and N2(t) represent the population of the two levels at any time t. Assuming that we have a total number of N atoms in the system, N = N1(t)+ N2(t) remains constant. This also implies that the rates above are identical but opposite in sign (you can check this in the equations)! Since a laser requires a population inversion to work, it is most useful to express the population difference at any time t as ΔN = N1(t)- N2(t) (redefined later in this chapter). When this number is less than zero, we have an inversion. We can now solve for the rate of change of the population difference as
 (1.6)
(1.6)
But the probability of an absorption is the same as the probability of a stimulated emission (i.e., W12 = W21 at the same intensity of incident photons),4 so that we may now express the equation as
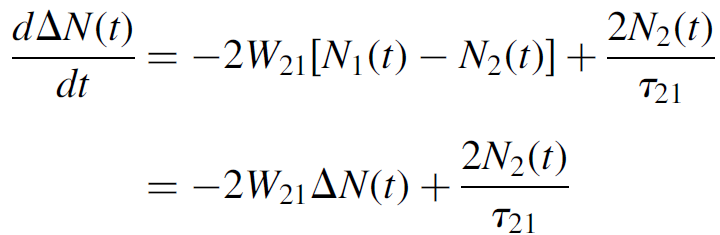 (1.7)
(1.7)
Furthermore, the total population of the system (N0) remains constant with N0 = N1(t)+ N2(t), so we may substitute ΔN(t)= N0 - 2N2(t), where the “×2” factor arises from the fact that a decrease of one atom from N2 results in an increase of one atom in level N1, so that the total change in the difference ΔN two atoms.
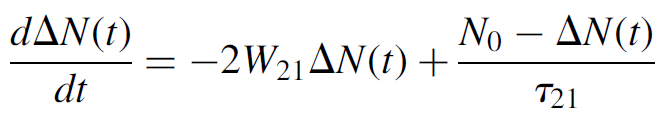 (1.8)
(1.8)
The rate at which the population difference occurs, then, is proportional to W21, which in turn is proportional to the incident light intensity (a higher incident stream of photons leads to a higher rate of stimulated emission). At steady state, though, the rate of change of population difference is zero, so equation (1.8) may be solved as
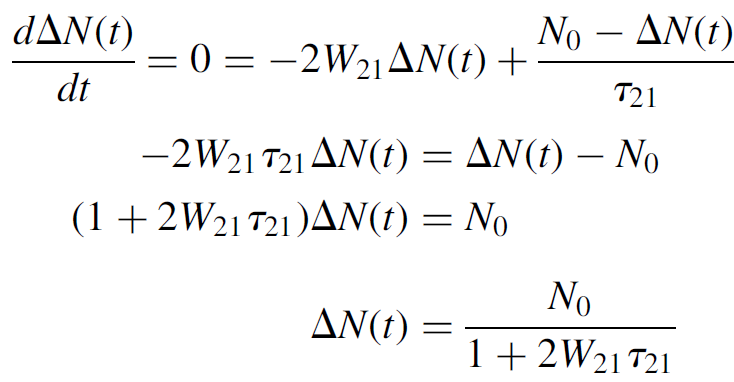 (1.9)
(1.9)
At low pump powers W21 tends toward zero, so the population difference is simply that of the number of atoms in the system (i.e., there are no excited atoms and the entire population is at level 1). At high pump powers the W21 term becomes large, so ΔN(t) tends toward zero. In other words, strong pumping will bring one half of the atomic population to the upper level and one-half to the lower level, so that there is no population difference. The atomic population of each level at various pump power levels is plotted in Figure 1.2, with N1 starting at N0 (the total
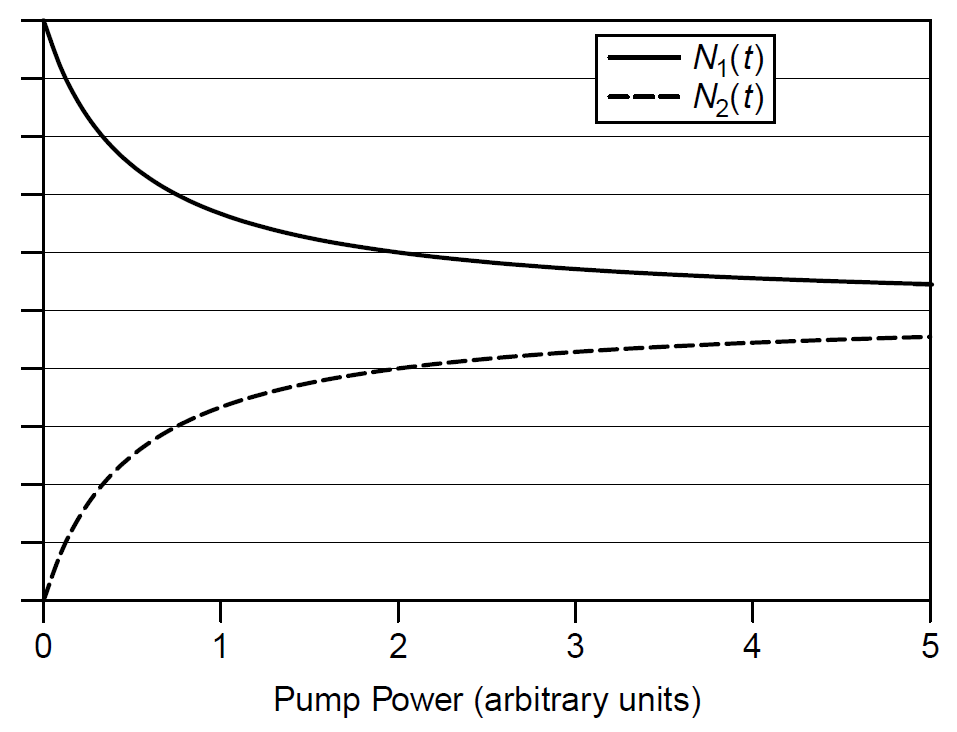
Figure 1.2. Energy-level populations for a two-level system.
number of atoms in the system) at zero pump power. In other words, there is no population at level N2; in reality, N2 would be thermally populated according to Boltzmann statistics, but for most systems this population would be negligible. Under no conditions can an inversion be achieved in this two-level system, so laser action is not possible with a two-level atomic system; to obtain laser action, a system with more than two related energy levels is required. Another useful parameter to define is the saturation intensity, the intensity of the incident photon stream at which the rate of stimulated emission is equal to the rate of spontaneous emission.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|