


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 26-1-2017
Date: 16-12-2015
Date: 16-12-2015
|
Longitudinal Motion
In discussing the properties of horizons, we have repeatedly run into the idea of the stretched horizon, located a microscopic distance above the mathematical horizon. It is natural to ask if the stretched horizon has any reality or whether it is just a mathematical fiction? Of course, to a Frefo observer, neither the stretched nor the mathematical horizon appears real. But to a Fido the stretched horizon is the layer containing the physical degrees of freedom that give rise to the entropy of the horizon. Thus, consistency requires that in some appropriate sense, the degrees of freedom of an infalling object should get deposited in this layer of finite thickness. To study this question we must examine how strings move in the X− direction.
It is a curious property of string theory that X−(σ) is not an independent degree of freedom. The only degrees of freedom carried by the string are the transverse coordinates Xi(σ) which lie in the plane of the horizon. The longitudinal location is defined by an equation whose origin is in the gauge fixing to the light cone gauge. The derivation is provided in the supplement that follows this discussion.
 (1.1)
(1.1)
Recall that the quantum theory of X(σ) is a simple (1+1 dimensional) quantum field theory of (D-2) free scalar fields defined on a unit circle. In such a theory, local operators can be characterized by a mass dimension. For example, Xi has dimension zero, while ∂Xi/∂σ has dimension 1. The right side of equation 1.1 has dimension 2. Thus it is apparent that X−(σ) has dimension 1. It immediately follows that the fluctuation in X− satisfies
 (1.2)
(1.2)
The factor ℓ2s is needed for dimensional reasons.
Another way to write equation 1.2 is to observe that δ is an averaging time in light cone coordinates. In other words δ = ΔX+. Equation 1.2 then takes the form of an uncertainty principle
 (1.3)
(1.3)
Now the geometric meaning of equation 1.3 is very interesting. Let us draw the motion of the fluctuating string in the X± plane as it falls towards

Fig. 1.1. Near horizon Rindler time slices.
the horizon. Evidently as X+ tends to zero the fluctuation in X− required by equation 1.3 must increase. This is shown in Figure 1.1. What the figure illustrates is that the stringy material tends to fill a region out to a fixed proper distance from the mathematical horizon at X+ = 0. In other words, unlike a point particle, the stringy substance is seen by a probe t hover at a distance ∼ ℓs above the horizon. Once again this surprising result is a direct consequence of arbitrarily high frequency fluctuations implicit in the stringy structure of matter. Note that if the string coupling satisfies gs << 1, the string length ℓs can be much greater than the Planck length, ℓP = ℓsg. In this case it is the string length and not the Planck length that controls the distance of the stretched horizon from the mathematical horizon.
___________________________________________________________
Supplement: Light cone gauge fixing of longitudinal string motions
The coordinate X−(τ, σ) is not an independent degree of freedom, but is given by equation 1.1. To see this multiply 1.1 by 1 = ∂X+/∂τ , which is true for light cone coordinates. Thus we must check the validity of the following equation
 (1.4)
(1.4)
The content of this equation expresses the underlying invariance of string theory to a reparameterization of the σ coordinate. Under the transformation
σ → σ + δσ
the X's transform as
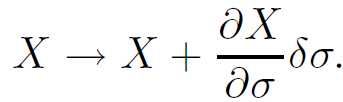 (1.5)
(1.5)
The Noether charge for this invariance is exactly the quantity in equation 1.4. Setting this quantity to zero insures that the physical spectrum consists only of states which are invariant under σ reparameterization. In going to the light cone frame the constraint serves to define X− in terms of the transverse coordinates. However even in the light cone gauge there is a bit of residual gauge invariance, namely shifting σ by a constant. In the light cone frame only the transverse X's are dynamical and the generator of these rigid shifts is

Fig. 1.2. String parameter translational invariance.
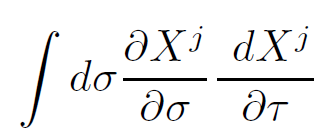 (1.6)
(1.6)
which by equation 1.1 is equal to
 (1.7)
(1.7)
Setting this to zero simultaneously insures invariance under shifts of σ and periodicity of X−(σ).



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|