


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 26-1-2017
Date: 16-12-2015
Date: 22-12-2015
|
Light Cone String Theory
Although naive pertubative string theory cannot capture this effect completely correctly, the tendency is already there in the theory of free strings. A free string is a generalization of a free particle. There are a number of excellent textbooks on string theory that the reader who is interested in technical details can consult. For our purposes, only the most elementary aspects of string theory will be needed.
A string is a one-dimensional continuum whose points are parameterized by a continuous parameter σ1. The transverse coordinates of the point at σ1 are labeled Xi(σ), where σ1 runs from 0 to 2π. It is also a function of a time-like parameter σ0, which is identified with light cone time X+. Thus Xi(σ0, σ1) is a field defined on a 1+1 dimensional parameter space (σa). In addition to Xi(σ), the canonical momentum density Pi(σ) can also be defined. At equal times X and P satisfy
 (1.1)
(1.1)
The light cone Hamiltonian for the free string is a natural generalization of that for a free particle;
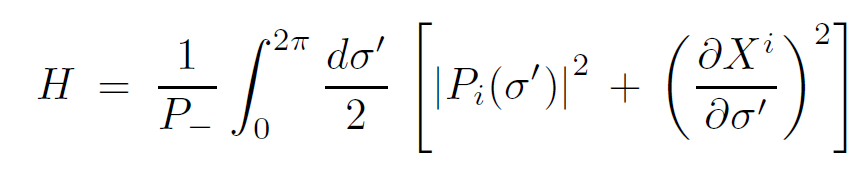 (1.2)
(1.2)
We have used units in which the string tension (energy per unit length in the rest frame) is unity.
The equation of motion following from equations 1.1 and 1.2 is a simple wave equation
 (1.3)
(1.3)
Quantization of the string is straightforward. Xi(σ) becomes a free scalar field in 1+1 dimensions satisfying equation 1.3 with periodic boundary conditions in σ1, X(σ0, 2π) = X(σ0, 0).
The string differs in important ways from the free particle, especially in its short time behavior. As we have repeatedly emphasized, it is the short time behavior that is key to complementarity.
Let us consider the analog of the question that we addressed about the time averaged location of the point particle. Now we consider the time averaged location of a point on the string. Thus, define
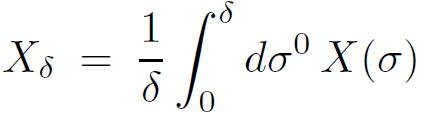 (1.4)
(1.4)
Since all points σ1 are equivalent, it doesn't matter what value σ1 takes on the right hand side when we evaluate Xδ. A useful measure of how much the information in a string is spread as it falls towards the horizon is provided by the fluctuations in Xδ, that is
 (1.5)
(1.5)
The state used for the expectation value in equation 1.5 is the ground state string. This quantity is easily calculated and diverges logarithmically as δ → 0. In other words, as the string approaches the horizon, any experiment (from the outside) to determine how its internal parts are distributed will indicate a logarithmic increase in the area it occupies
(ΔX)2 ∼ |log δ |. (1.6)
Another way to write equation 1.6 is to use the connection between Rindler time and light cone time
(ΔX)2 ∼ |log (2Le-2τ )| ∼ 2τ.
Finally, we can use the relation between Rindler time and Schwarzschild time given by τ = t/4MG to obtain
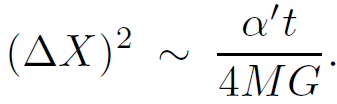 (1.7)
(1.7)
In equation 1.7 we have restored the units by including the factor α', the inverse string tension.
Here we see the beginnings of an explanation of complementarity. The observer outside the black hole will find the string diffusing over an increasing area of the horizon as time progresses. But an observer falling with the string and doing low energy experiments on it would conclude that the string remains a fixed finite size as it falls.
The linear growth of the area in equation 1.7 is much slower than the growth of a charged particle. A completely consistent theory would require these growth patterns to match. The true exponential asymptotic growth is undoubtedly a non-perturbative phenomenon that involves string interactions in an essential way.
To see how interactions influence the evolution, let's determine the average total length of string, projected onto the two-dimensional transverse plane
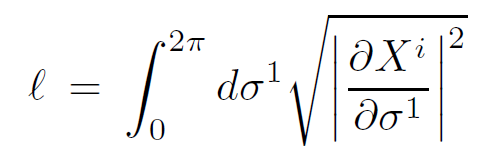 (1.8)
(1.8)
As a preliminary, let us consider the ground state average of |∂Xi /∂σ1|2. This is another exercise in free scalar quantum field theory, and the result is quadratically divergent.
If however ∂Xi /∂σ is averaged over the time interval δ, we find that the ground state average of |∂Xi /∂σ1|2 is given by
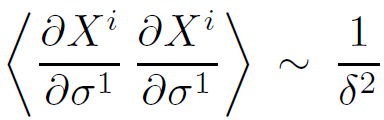 (1.9)
(1.9)
Using the fact that the probability distribution for ∂Xi/∂σ1 is Gaussian in free field theory, we can conclude that or ℓ scales as
or ℓ scales as
 (1.10)
(1.10)
or
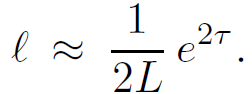 (1.11)
(1.11)
In other words, as the string falls toward the horizon, it grows exponentially in length.
Another quantity which exponentially grows is the ρ component of the Rindler momentum. To see this, we use the transformation to derive

or in terms of momenta
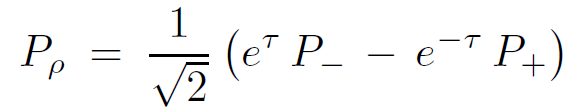 (1.12)
(1.12)
In the Rindler approximation to a black hole horizon, P± are conserved, and therefore as τ →∞ the radial momentum Pρ grows like eτ. Evidently then the ratio of the string length to its total radial momentum is fixed. As the string falls toward the horizon, its radial momentum increases by the mechanism of its physical length increasing.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
نقابة تمريض كربلاء تشيد بمستشفى الكفيل وتؤكّد أنّها بيئة تدريبية تمتلك معايير النجاح
|
|
|