


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-02-04
التاريخ: 15-9-2020
التاريخ: 13-9-2020
التاريخ: 19-2-2016
|
Let us consider what determines the constants A and B, or a and Δ. Of course, these are determined by how we start the motion. If we start the motion with just a small displacement, that is one type of oscillation; if we start with an initial displacement and then push up when we let go, we get still a different motion. The constants A and B, or a and Δ, or any other way of putting it, are determined, of course, by the way the motion started, not by any other features of the situation. These are called the initial conditions. We would like to connect the initial conditions with the constants. Although this can be done using any one of the forms (21.6), it turns out to be easiest if we use Eq. (21.6c).
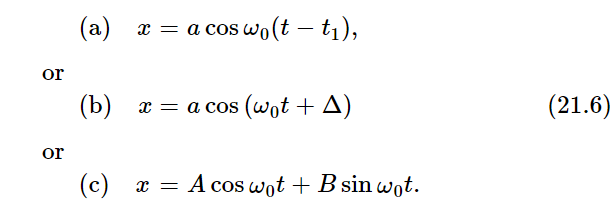
Suppose that at t=0 we have started with an initial displacement x0 and a certain velocity v0. This is the most general way we can start the motion. (We cannot specify the acceleration with which it started, true, because that is determined by the spring, once we specify x0.) Now let us calculate A and B. We start with the equation for x,
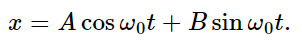
Since we shall later need the velocity also, we differentiate x and obtain

These expressions are valid for all t, but we have special knowledge about x and v at t=0. So, if we put t=0 into these equations, on the left we get x0 and v0, because that is what x and v are at t=0; also, we know that the cosine of zero is unity, and the sine of zero is zero. Therefore, we get
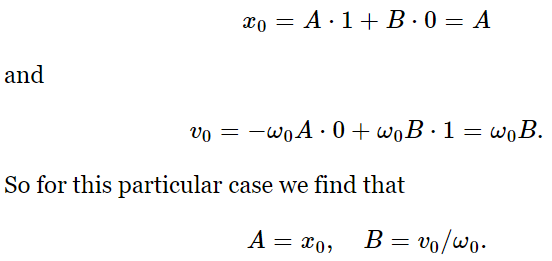
From these values of A and B, we can get a and Δ if we wish.
That is the end of our solution, but there is one physically interesting thing to check, and that is the conservation of energy. Since there are no frictional losses, energy ought to be conserved. Let us use the formula
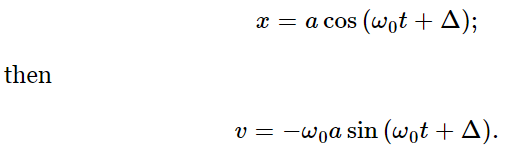
Now let us find out what the kinetic energy T is, and what the potential energy U is. The potential energy at any moment is 1/2 kx2, where x is the displacement and k is the constant of the spring. If we substitute for x, using our expression above, we get
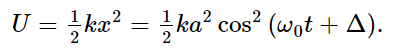
Of course, the potential energy is not constant; the potential never becomes negative, naturally—there is always some energy in the spring, but the amount of energy fluctuates with x. The kinetic energy, on the other hand, is 1/2 mv2, and by substituting for v we get
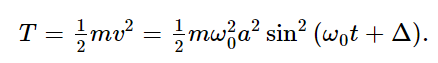
Now the kinetic energy is zero when x is at the maximum, because then there is no velocity; on the other hand, it is maximal when x is passing through zero, because then it is moving fastest. This variation of the kinetic energy is just the opposite of that of the potential energy. But the total energy ought to be a constant. If we note that k=mω20, we see that
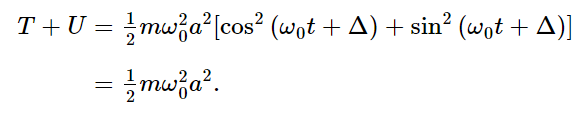
The energy is dependent on the square of the amplitude; if we have twice the amplitude, we get an oscillation which has four times the energy. The average potential energy is half the maximum and, therefore, half the total, and the average kinetic energy is likewise half the total energy.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
مؤسسة السجناء السياسيين: سجلنا 120 ألفًا من ضحايا السجون والاعتقالات في عهد النظام السابق
|
|
|