


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 19-2-2016
التاريخ: 13-9-2020
التاريخ: 1-1-2017
التاريخ: 13-9-2020
|
All the foregoing examples are simple cases where the bodies collide and stick together, or were initially stuck together and later separated by an explosion. However, there are situations in which the bodies do not cohere, as, for example, two bodies of equal mass which collide with equal speeds and then rebound. For a brief moment they are in contact and both are compressed. At the instant of maximum compression, they both have zero velocity and energy is stored in the elastic bodies, as in a compressed spring. This energy is derived from the kinetic energy the bodies had before the collision, which becomes zero at the instant their velocity is zero. The loss of kinetic energy is only momentary, however. The compressed condition is analogous to the cap that releases energy in an explosion. The bodies are immediately decompressed in a kind of explosion, and fly apart again; but we already know that case—the bodies fly apart with equal speeds. However, this speed of rebound is less, in general, than the initial speed, because not all the energy is available for the explosion, depending on the material. If the material is putty no kinetic energy is recovered, but if it is something more rigid, some kinetic energy is usually regained. In the collision the rest of the kinetic energy is transformed into heat and vibrational energy—the bodies are hot and vibrating. The vibrational energy also is soon transformed into heat. It is possible to make the colliding bodies from highly elastic materials, such as steel, with carefully designed spring bumpers, so that the collision generates very little heat and vibration. In these circumstances the velocities of rebound are practically equal to the initial velocities; such a collision is called elastic.
That the speeds before and after an elastic collision are equal is not a matter of conservation of momentum, but a matter of conservation of kinetic energy. That the velocities of the bodies rebounding after a symmetrical collision are equal to and opposite each other, however, is a matter of conservation of momentum.
We might similarly analyze collisions between bodies of different masses, different initial velocities, and various degrees of elasticity, and determine the final velocities and the loss of kinetic energy, but we shall not go into the details of these processes.
Elastic collisions are especially interesting for systems that have no internal “gears, wheels, or parts.” Then when there is a collision there is nowhere for the energy to be impounded, because the objects that move apart are in the same condition as when they collided. Therefore, between very elementary objects, the collisions are always elastic or very nearly elastic. For instance, the collisions between atoms or molecules in a gas are said to be perfectly elastic. Although this is an excellent approximation, even such collisions are not perfectly elastic; otherwise, one could not understand how energy in the form of light or heat radiation could come out of a gas. Once in a while, in a gas collision, a low-energy infrared ray is emitted, but this occurrence is very rare and the energy emitted is very small. So, for most purposes, collisions of molecules in gases are considered to be perfectly elastic.
As an interesting example, let us consider an elastic collision between two objects of equal mass. If they come together with the same speed, they would come apart at that same speed, by symmetry. But now look at this in another circumstance, in which one of them is moving with velocity v and the other one is at rest. What happens? We have been through this before. We watch the symmetrical collision from a car moving along with one of the objects, and we find that if a stationary body is struck elastically by another body of exactly the same mass, the moving body stops, and the one that was standing still now moves away with the same speed that the other one had; the bodies simply exchange velocities. This behavior can easily be demonstrated with a suitable impact apparatus. More generally, if both bodies are moving, with different velocities, they simply exchange velocity at impact.
Another example of an almost elastic interaction is magnetism. If we arrange a pair of U-shaped magnets in our glide blocks, so that they repel each other, when one drifts quietly up to the other, it pushes it away and stands perfectly still, and now the other goes along, frictionlessly.
The principle of conservation of momentum is very useful, because it enables us to solve many problems without knowing the details. We did not know the details of the gas motions in the cap explosion, yet we could predict the velocities with which the bodies came apart, for example. Another interesting example is rocket propulsion. A rocket of large mass, M, ejects a small piece, of mass m, with a terrific velocity V relative to the rocket. After this the rocket, if it were originally standing still, will be moving with a small velocity, v. Using the principle of conservation of momentum, we can calculate this velocity to be
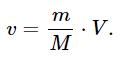
So long as material is being ejected, the rocket continues to pick up speed. Rocket propulsion is essentially the same as the recoil of a gun: there is no need for any air to push against.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|