


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-1-2022
Date: 2-2-2016
Date: 26-12-2021
|
Let 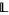 be a lattice (or a bounded lattice or a complemented lattice, etc.), and let
be a lattice (or a bounded lattice or a complemented lattice, etc.), and let 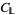 be the covering relation of
be the covering relation of 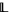 :
:
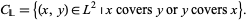 |
Then 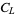 is locally realized provided that for every finite subset
is locally realized provided that for every finite subset 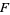 of
of 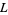 , there is a finitely generated sublattice
, there is a finitely generated sublattice 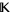 of
of 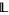 , that contains
, that contains 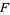 , for which
, for which 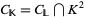 . It can be shown that
. It can be shown that 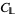 is locally realized if and only if there is a hyperfinitely generated sublattice
is locally realized if and only if there is a hyperfinitely generated sublattice 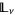 of
of 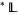 such that
such that 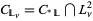 . Using this characterization of locally realized covering relations, the following standard result can be proved using nonstandard methods:
. Using this characterization of locally realized covering relations, the following standard result can be proved using nonstandard methods:
Let 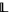 be a locally finite lattice in which the covering relation is locally realized, and let
be a locally finite lattice in which the covering relation is locally realized, and let 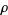 be the sublattice of
be the sublattice of 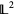 which is generated by
which is generated by 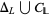 . Then
. Then 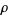 is a connected tolerance of
is a connected tolerance of 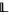 , and it is in fact the smallest locally subconnected (and locally connected) tolerance of
, and it is in fact the smallest locally subconnected (and locally connected) tolerance of 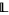 .
.
REFERENCES:
Burris, S. and Sankappanavar, H. P. A Course in Universal Algebra. New York: Springer-Verlag, 1981. http://www.thoralf.uwaterloo.ca/htdocs/ualg.html.
Gehrke, M.; Kaiser, K.; and Insall, M. "Some Nonstandard Methods Applied to Distributive Lattices." Zeitschrifte für Mathematische Logik und Grundlagen der Mathematik 36, 123-131, 1990.
Grätzer, G. Lattice Theory: First Concepts and Distributive Lattices. San Francisco, CA: W. H. Freeman, 1971.
Grätzer, G. Universal Algebra, 2nd ed. New York: Springer-Verlag, 1979.
Insall, M. "Some Finiteness Conditions in Lattices Using Nonstandard Proof Methods." J. Austral. Math. Soc. 53, 266-280, 1992.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|