Infinity

Infinity, most often denoted as , is an unbounded quantity that is greater than every real number. The symbol 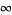 had been used as an alternative to M (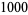) in Roman numerals until 1655, when John Wallis suggested it be used instead for infinity.

Infinity is a very tricky concept to work with, as evidenced by some of the counterintuitive results that follow from Georg Cantor's treatment of infinite sets.

Informally, 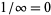, a statement that can be made rigorous using the limit concept,

Similarly,

where the notation  indicates that the limit is taken from the positive side of the real line.

In the Wolfram Language,  is represented using the symbol Infinity.

REFERENCES:

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 19, 1996.

Courant, R. and Robbins, H. "The Mathematical Analysis of Infinity." §2.4 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 77-88, 1996.

Hardy, G. H. Orders of Infinity: The 'infinitarcalcul' of Paul Du Bois-Reymond, 2nd ed. Cambridge, England: Cambridge University Press, 1924.

Lavine, S. Understanding the Infinite. Cambridge, MA: Harvard University Press, 1994.

Maor, E. To Infinity and Beyond: A Cultural History of the Infinite. Boston, MA: Birkhäuser, 1987.

Moore, A. W. The Infinite. New York: Routledge, 1991.

Morris, R. Achilles in the Quantum Universe: The Definitive History of Infinity. New York: Henry Holt, 1997.

Owen, H. P. "Infinity in Theology and Metaphysics." In The Encyclopedia of Philosophy, Vol. 4. New York: Crowell Collier, pp. 190-193, 1967.

Péter, R. Playing with Infinity. New York: Dover, 1976.

Rucker, R. Infinity and the Mind: The Science and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1995.

Smail, L. L. Elements of the Theory of Infinite Processes. New York: McGraw-Hill, 1923.

Thomson, J. "Infinity in Mathematics and Logic." In The Encyclopedia of Philosophy, Vol. 4. New York: Crowell Collier, pp. 183-190, 1967.

Vilenskin, N. Ya. In Search of Infinity. Boston, MA: Birkhäuser, 1995.

Weisstein, E. W. "Books about Infinity." http://www.ericweisstein.com/encyclopedias/books/Infinity.html.

Wilson, A. M. The Infinite in the Finite. New York: Oxford University Press, 1996.

Zippin, L. Uses of Infinity. New York: Random House, 1962.