


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-5-2021
Date: 20-5-2021
Date: 27-5-2021
|
The word net has several meanings in mathematics. It refers to a plane diagram in which the polyhedron edges of a polyhedron are shown, a point set satisfying certain uniformity of distribution conditions, and a topological generalization of a sequence.
 |
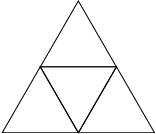 |
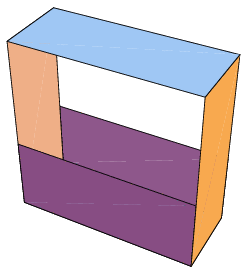
The net of a polyhedron is also known as a development, pattern, or planar net (Buekenhout and Parker 1998). The illustrations above show polyhedron nets for the cube and tetrahedron.
In his classic Treatise on Measurement with the Compass and Ruler, Dürer (1525) made one of the first presentations of a net (Livio 2002, p. 138).
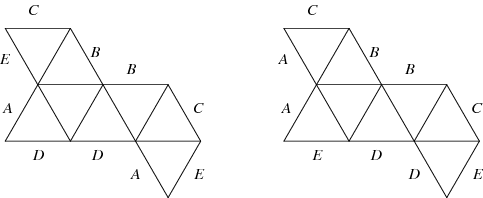
The net of a polyhedron must in general also specify which edges are to be joined since there might be ambiguity as to which of several possible polyhedra a net might fold into. For simple symmetrical polyhedra, the folding procedure can only be done one way, so edges need not be labeled. However, for the net shown above, two different solids can be constructed from the same net: the boat for the left figure and the octahedron for the right figure.
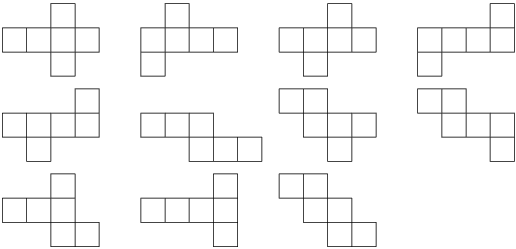
Polyhedron nets are not unique. For example, there are a total of 11 distinct nets for the cube (Buekenhout and Parker 1998, Malkevitch), illustrated above. Buekenhout and Parker (1998) compute the number of nets for all regular convex polytopes in dimension 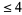 . The results for the Platonic solids are summarized in the table below. For the Platonics, duals have the same numbers of unfoldings as their base solids (Buekenhout and Parker 1998).
. The results for the Platonic solids are summarized in the table below. For the Platonics, duals have the same numbers of unfoldings as their base solids (Buekenhout and Parker 1998).
| Platonic solid | number of nets |
| cube | 11 |
| dodecahedron | 43380 |
| icosahedron | 43380 |
| octahedron | 11 |
| tetrahedron | 2 |
 |
 |
Not every plane diagram that resembles a net actually corresponds to a closed surface. For example, the "net" shown above corresponds to a basket with a handle but not a polyhedron.
Each net is uniquely determined by a spanning tree of the 1-skeleton of the polyhedron, i.e., the edges which are cut form a spanning tree of the vertices-edges graph (Buekenhout and Parker 1998).
It is conjectured (but amazingly not proved) that all convex polyhedra have nets (Shephard 1975, Malkevitch), a statement sometimes known as Shephard's conjecture.
Not all concave polyhedra do (the constituent polygons can overlap one another when a concave polyhedron is flattened out). The great dodecahedron and stella octangula are examples of a concave polyhedron which have nonself-intersecting nets. K. Fukuda has written routines which can unfold convex polyhedra into a planar net.
A 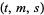 -net is a set of
-net is a set of 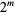
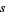 -dimensional points such that every half-open interval with volume
-dimensional points such that every half-open interval with volume 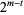 contains exactly
contains exactly 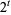 points. The Hammersley point set with
points. The Hammersley point set with 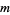 even and
even and 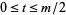 forms a
forms a 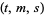 net.
net.
The term net also has a technical meaning as a generalization of a sequence, in which context it is also known as a Moore-Smith sequence. In this context, nets are used in general topology and analysis to imbue non-metrizable topological spaces with convergence properties. This artifice is needed only in spaces which are not first-countable, since sequences alone provide an adequate way of dealing with continuity for first-countable spaces. Nets are used in the study of the Riemann integral. Formally, a net of a set 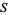 is a mapping from a directed set
is a mapping from a directed set 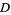 into
into 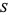 .
.
REFERENCES:
Bell Laboratories. https://netlib.bell-labs.com/netlib/polyhedra/.
Bouzette, S.; Buekenhout, F.; Edmond, D.; Gottcheiner, A. "A Theory of Nets for Polyhedra and Polytopes Related to Incidence Geometry." Designs, Codes and Cryptography 10, 115-136, 1997.
Buekenhout, F. and Parker, M. "The Number of Nets of the Regular Convex Polytopes in Dimension 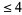 ." Disc. Math. 186, 69-94, 1998.
." Disc. Math. 186, 69-94, 1998.
Dürer, A. Unterweisung der Messung mit dem Zirkel und Richtscheit. 1525.
Fukuda, K. UnfoldPolytope Mathematica packages. https://www.cs.mcgill.ca/~fukuda/download/mathematica/.
Grünbaum, B. "Nets of Polyhedra." Geombinatorics 1, No. 2, 5-10, 1991.
Grünbaum, B. "Nets of Polyhedra II." Geombinatorics 1, No. 3, 5-10, 1991.
Grünbaum, B. "A Starshaped Polyhedron with No Net." Geombinatorics 11, 43-48, 2001.
Livio, M. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books, 2002.
Malkevitch, J. "Nets: A Tool for Representing Polyhedra in Two Dimensions." https://www.ams.org/new-in-math/cover/nets.html.
Malkevitch, J. "Unfolding Polyhedra." https://www.york.cuny.edu/~malk/unfolding.html.
Malkevitch, J. "Le géométrie et la paire de ciseaux." La Recherche. No. 346, Oct. 2001. https://www.larecherche.fr/special/web/web346.html.
Schlickenrieder, W. Nets of Polyhedra. Ph.D. thesis. Berlin: Technische Universität Berlin, 1997.
Shephard, G. C. "Convex Polytopes with Convex Nets." Math. Proc. Camb. Phil. Soc. 78, 389-403, 1975.
Weisstein, E. W. "Polyhedron Nets on MathWorld." https://mathworld.wolfram.com/topics/PolyhedronNets.html.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|