


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2021
Date: 13-5-2021
Date: 13-7-2021
|
A set 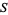 is discrete in a larger topological space
is discrete in a larger topological space 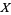 if every point
if every point 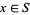 has a neighborhood
has a neighborhood 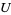 such that
such that 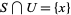 . The points of
. The points of 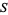 are then said to be isolated (Krantz 1999, p. 63). Typically, a discrete set is either finite or countably infinite. For example, the set of integers is discrete on the real line. Another example of an infinite discrete set is the set
are then said to be isolated (Krantz 1999, p. 63). Typically, a discrete set is either finite or countably infinite. For example, the set of integers is discrete on the real line. Another example of an infinite discrete set is the set 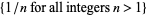 . On any reasonable space, a finite set is discrete. A set is discrete if it has the discrete topology, that is, if every subset is open.
. On any reasonable space, a finite set is discrete. A set is discrete if it has the discrete topology, that is, if every subset is open.
In the case of a subset 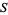 , as in the examples above, one uses the relative topology on
, as in the examples above, one uses the relative topology on 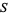 . Sometimes a discrete set is also closed. Then there cannot be any accumulation points of a discrete set. On a compact set such as the sphere, a closed discrete set must be finite because of this.
. Sometimes a discrete set is also closed. Then there cannot be any accumulation points of a discrete set. On a compact set such as the sphere, a closed discrete set must be finite because of this.
REFERENCES:
Krantz, S. G. "Discrete Sets and Isolated Points." §4.6.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 63-64, 1999.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|