Stokes' Theorem

For 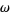 a differential (k-1)-form with compact support on an oriented 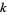-dimensional manifold with boundary ,

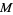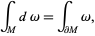(1)

where 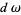 is the exterior derivative of the differential form 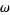. When  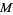is a compact manifold without boundary, then the formula holds with the right hand side zero.

Stokes' theorem connects to the "standard" gradient, curl, and divergence theorems by the following relations. If 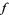 is a function on ,

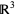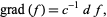(2)

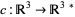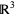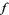where  (the dual space) is the duality isomorphism between a vector space and its dual, given by the Euclidean inner product on . If  is a vector field on a ,

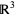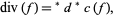(3)

where 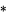 is the Hodge star operator. If  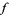is a vector field on ,

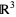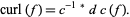(4)

With these three identities in mind, the above Stokes' theorem in the three instances is transformed into the gradient, curl, and divergence theorems respectively as follows. If 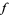 is a function on  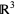and 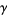 is a curve in 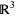, then

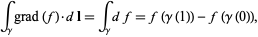(5)

which is the gradient theorem. If 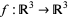 is a vector field and  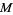an embedded compact 3-manifold with boundary in 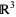, then

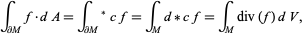(6)

which is the divergence theorem. If 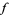 is a vector field and  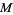is an oriented, embedded, compact 2-manifold with boundary in 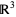, then

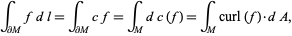(7)

which is the curl theorem.

de Rham cohomology is defined using differential k-forms. When 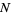 is a submanifold (without boundary), it represents a homology class. Two closed forms represent the same cohomology class if they differ by an exact form, 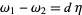. Hence,

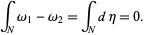(8)

Therefore, the evaluation of a cohomology class on a homology class is well-defined.

Physicists generally refer to the curl theorem

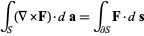(9)

as Stokes' theorem.

REFERENCES:

Morse, P. M. and Feshbach, H. "Stokes' Theorem." In Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 43, 1953.