


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-7-2021
Date: 14-7-2021
Date: 11-8-2021
|
A knot 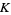 in
in 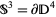 is a slice knot if it bounds a disk
is a slice knot if it bounds a disk 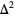 in
in 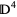 which has a tubular neighborhood
which has a tubular neighborhood 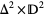 whose intersection with
whose intersection with 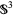 is a tubular neighborhood
is a tubular neighborhood 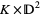 for
for 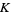 .
.
Every ribbon knot is a slice knot, and it is conjectured that every slice knot is a ribbon knot.
The knot determinant of a slice knot is a square number (Rolfsen 1976, p. 224).
 |
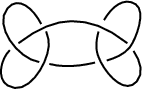 |
Slice knots include the unknot (Rolfsen 1976, p. 226), square knot (Rolfsen 1976, p. 220), stevedore's knot 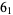 , and
, and  (Rolfsen 1976, p. 225), illustrated above.
(Rolfsen 1976, p. 225), illustrated above.
Casson and Gordon (1975) showed that the unknot and stevedore's knot are the only twist knots that are slice knots (Rolfsen 1976, p. 226).
REFERENCES:
Casson, J. and Gordon, C. M. "Cobordism of Classical Knots." Preprint of Lecture. Orsay. 1975.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 218-220, 1976.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|