
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-3-2021
Date: 15-2-2021
Date: 16-2-2021
|
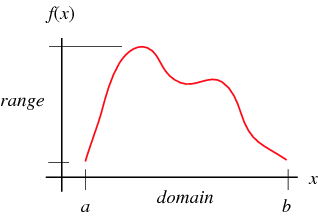
If 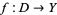 is a map (a.k.a. function, transformation, etc.) over a domain
is a map (a.k.a. function, transformation, etc.) over a domain 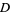 , then the range of
, then the range of 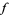 , also called the image of
, also called the image of 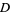 under
under 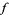 , is defined as the set of all values that
, is defined as the set of all values that 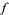 can take as its argument varies over
can take as its argument varies over 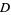 , i.e.,
, i.e.,
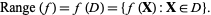 |
Note that among mathematicians, the word "image" is used more commonly than "range."
The range is a subset of 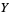 and does not have to be all of
and does not have to be all of 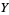 .
.
Unfortunately, term "range" is often used to mean domain--its precise opposite--in probability theory, with Feller (1968, p. 200) and Evans et al. (2000, p. 5) calling the set of values that a variate 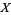 can assume (i.e., the set of values
can assume (i.e., the set of values  that a probability density function
that a probability density function 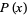 is defined over) the "range", denoted by
is defined over) the "range", denoted by 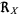 (Evans et al. 2000, p. 5).
(Evans et al. 2000, p. 5).
Even worse, statistics most commonly uses "range" to refer to the completely different statistical quantity as the difference between the largest and smallest order statistics. In this work, this form of range is referred to as "statistical range."
REFERENCES:
Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, 2000.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|