


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-5-2021
Date: 15-4-2021
Date: 19-2-2021
|
A class of formal series expansions in derivatives of a distribution 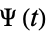 which may (but need not) be the normal distribution function
which may (but need not) be the normal distribution function
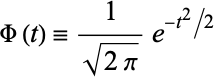 |
(1) |
and moments or other measured parameters. Edgeworth series are known as the Charlier series or Gram-Charlier series. Let 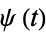 be the characteristic function of the function
be the characteristic function of the function 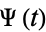 , and
, and 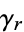 its cumulants. Similarly, let
its cumulants. Similarly, let 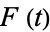 be the distribution to be approximated,
be the distribution to be approximated, 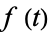 its characteristic function, and
its characteristic function, and 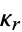 its cumulants. By definition, these quantities are connected by the formal series
its cumulants. By definition, these quantities are connected by the formal series
![f(t)=exp[sum_(r=1)^infty(kappa_r-gamma_r)((it)^r)/(r!)]psi(t)](https://mathworld.wolfram.com/images/equations/CharlierSeries/NumberedEquation2.gif) |
(2) |
(Wallace 1958). Integrating by parts gives 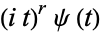 as the characteristic function of
as the characteristic function of 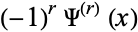 , so the formal identity corresponds pairwise to the identity
, so the formal identity corresponds pairwise to the identity
![F(x)=exp[sum_(r=1)^infty(kappa_r-gamma_r)((-D)^r)/(r!)]Psi(x),](https://mathworld.wolfram.com/images/equations/CharlierSeries/NumberedEquation3.gif) |
(3) |
where 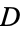 is the differential operator. The most important case
is the differential operator. The most important case 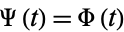 was considered by Chebyshev (1890), Charlier (1905-06), and Edgeworth (1905).
was considered by Chebyshev (1890), Charlier (1905-06), and Edgeworth (1905).
Expanding and collecting terms according to the order of the derivatives gives the so-called Gram-Charlier A-Series, which is identical to the formal expansion of 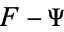 in Hermite polynomials. The A-series converges for functions
in Hermite polynomials. The A-series converges for functions 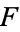 whose tails approach zero faster than
whose tails approach zero faster than 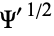 (Cramér 1925, Wallace 1958, Szegö 1975).
(Cramér 1925, Wallace 1958, Szegö 1975).
REFERENCES:
Charlier, C. V. L. "Über das Fehlergesetz." Ark. Math. Astr. och Phys. 2, No. 8, 1-9, 1905-06.
Chebyshev, P. L. "Sur deux théorèmes relatifs aux probabilités." Acta Math. 14, 305-315, 1890.
Cramér, H. "On Some Classes of Series Used in Mathematical Statistics." Proceedings of the Sixth Scandinavian Congress of Mathematicians, Copenhagen. pp. 399-425, 1925.
Edgeworth, F. Y. "The Law of Error." Cambridge Philos. Soc. 20, 36-66 and 113-141, 1905.
Gram, J. P. "Über die Entwicklung reeler Funktionen in Reihen mittelst der Methode der kleinsten Quadrate." J. reine angew. Math. 94, 41-73, 1883.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.
Wallace, D. L. "Asymptotic Approximations to Distributions." Ann. Math. Stat. 29, 635-654, 1958.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|