Euler's Number Triangle

The triangle of numbers 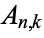 given by

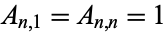(1)

and the recurrence relation

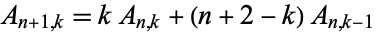(2)

for , where 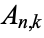 are shifted Eulerian numbers, i.e.,

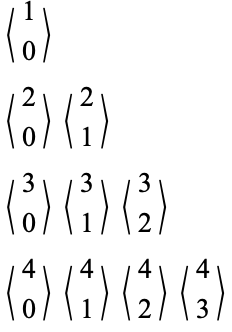(3)

(4)

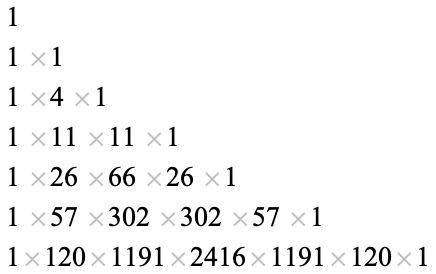
(OEIS A008292). Note that the rows sum to the successive factorials , , , , ....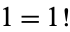

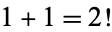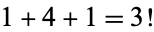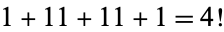The plot above shows the binary representations for the first 255 (top figure) and 511 (bottom figure) terms of a flattened Euler's number triangle.

Amazingly, the Z-transform of 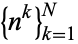 is the generator for the first  rows of Euler's number triangle, when the 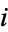th term of the transform is first cleared of its denominator by multiplying through by 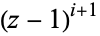. For example,

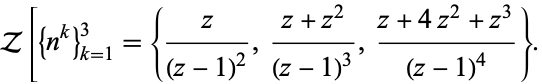(5)

REFERENCES:

Sloane, N. J. A. Sequence A008292 in "The On-Line Encyclopedia of Integer Sequences."