


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-7-2020
Date: 2-1-2020
Date: 5-1-2021
|
A generalization of the Fibonacci numbers defined by 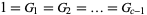 and the recurrence relation
and the recurrence relation
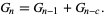 |
(1) |
These are the sums of elements on successive diagonals of a left-justified Pascal's triangle beginning in the leftmost column and moving in steps of 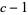 up and 1 right. The case
up and 1 right. The case 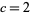 equals the usual Fibonacci number. These numbers satisfy the identities
equals the usual Fibonacci number. These numbers satisfy the identities
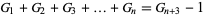 |
(2) |
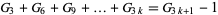 |
(3) |
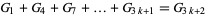 |
(4) |
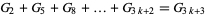 |
(5) |
(Bicknell-Johnson and Spears 1996). For the special case 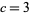 ,
,
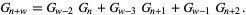 |
(6) |
Bicknell-Johnson and Spears (1996) give many further identities.
Horadam (1965) defined the generalized Fibonacci numbers 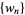 as
as 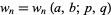 , where
, where 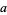 ,
, 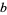 ,
, 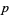 , and
, and 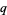 are integers,
are integers, 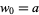 ,
, 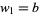 , and
, and 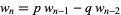 for
for 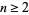 . They satisfy the identities
. They satisfy the identities
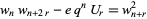 |
(7) |
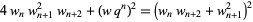 |
(8) |
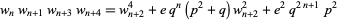 |
(9) |
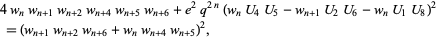 |
(10) |
where
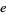 |
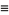 |
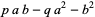 |
(11) |
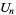 |
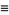 |
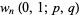 |
(12) |
(Dujella 1996). The final above result is due to Morgado (1987) and is called the morgado identity.
Another generalization of the Fibonacci numbers is denoted 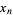 . Given
. Given 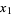 and
and 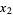 , define the generalized Fibonacci number by
, define the generalized Fibonacci number by 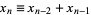 for
for 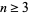 ,
,
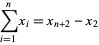 |
(13) |
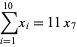 |
(14) |
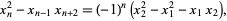 |
(15) |
where the plus and minus signs alternate.
REFERENCES:
Bicknell, M. "A Primer for the Fibonacci Numbers, Part VIII: Sequences of Sums from Pascal's Triangle." Fib. Quart. 9, 74-81, 1971.
Bicknell-Johnson, M. and Spears, C. P. "Classes of Identities for the Generalized Fibonacci Numbers 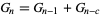 for Matrices with Constant Valued Determinants." Fib. Quart. 34, 121-128, 1996.
for Matrices with Constant Valued Determinants." Fib. Quart. 34, 121-128, 1996.
Dujella, A. "Generalized Fibonacci Numbers and the Problem of Diophantus." Fib. Quart. 34, 164-175, 1996.
Horadam, A. F. "Generating Functions for Powers of a Certain Generalized Sequence of Numbers." Duke Math. J. 32, 437-446, 1965.
Horadam, A. F. "Generalization of a Result of Morgado." Portugaliae Math. 44, 131-136, 1987a.
Horadam, A. F. and Shannon, A. G. "Generalization of Identities of Catalan and Others." Portugaliae Math. 44, 137-148, 1987b.
Morgado, J. "Note on Some Results of A. F. Horadam and A. G. Shannon Concerning a Catalan's Identity on Fibonacci Numbers." Portugaliae Math. 44, 243-252, 1987.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
الزائرون يحيون ليلة الجمعة الأخيرة من شهر ربيع الآخر عند مرقد أبي الفضل العبّاس (عليه السلام)
|
|
|