


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-10-2020
Date: 6-2-2020
Date: 6-5-2020
|
A Smarandache-like function which is defined where 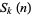 is defined as the smallest integer for which
is defined as the smallest integer for which 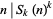 . The Smarandache
. The Smarandache 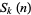 function can therefore be obtained by replacing any factors which are
function can therefore be obtained by replacing any factors which are 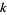 th powers in
th powers in 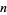 by their
by their 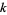 roots.
roots.
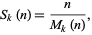 |
where 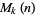 is the number of solutions to
is the number of solutions to 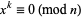 .
.
The functions 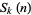 for
for 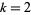 , 3, ..., 6 for values such that
, 3, ..., 6 for values such that 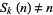 are tabulated by Begay (1997). The following table gives
are tabulated by Begay (1997). The following table gives 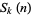 for small
for small 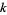 and
and 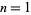 , 2, ....
, 2, ....
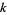 |
OEIS | 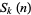 |
| 1 | A000027 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, ... |
| 2 | A019554 | 1, 2, 3, 2, 5, 6, 7, 4, 3, 10, 11, 6, 13, 14, 15, 4, 17, 6, ... |
| 3 | A019555 | 1, 2, 3, 2, 5, 6, 7, 2, 3, 10, 11, 6, 13, 14, 15, 4, 17, 6, ... |
| 4 | A053166 | 1, 2, 3, 2, 5, 6, 7, 2, 3, 10, 11, 6, 13, 14, 15, 2, 17, 6, ... |
REFERENCES:
Begay, A. "Smarandache Ceil Functions." Bull. Pure Appl. Sci. 16E, 227-229, 1997. https://www.gallup.unm.edu/~smarandache/smarceil.htm.
Sloane, N. J. A. Sequences A000027/M0472, A019554, A019555, and A053166 in "The On-Line Encyclopedia of Integer Sequences."
Smarandache, F. Collected Papers, Vol. 2. Kishinev, Moldova: Kishinev University Press, 1997.
Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993.
Weisstein, E. W. "Gigantic Primes with Prime Digits Found." MathWorld Headline News, Apr. 9, 2002. https://mathworld.wolfram.com/news/2002-04-09/primeprimes/.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|