


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-11-2020
Date: 27-2-2020
Date: 10-4-2020
|
The Erdős-Selfridge function 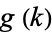 is defined as the least integer bigger than
is defined as the least integer bigger than 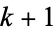 such that the least prime factor of
such that the least prime factor of 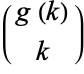 exceeds
exceeds 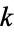 , where
, where 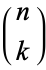 is the binomial coefficient (Ecklund et al. 1974, Erdős et al. 1993). The best lower bound known is
is the binomial coefficient (Ecklund et al. 1974, Erdős et al. 1993). The best lower bound known is
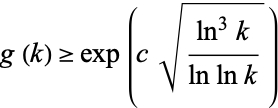 |
(Granville and Ramare 1996). Scheidler and Williams (1992) tabulated 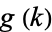 up to
up to 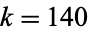 , and Lukes et al. (1997) tabulated
, and Lukes et al. (1997) tabulated 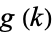 for
for 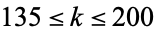 . The values for
. The values for 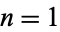 , 2, 3, ... are 3, 6, 7, 7, 23, 62, 143, 44, 159, 46, 47, 174, 2239, ... (OEIS A003458).
, 2, 3, ... are 3, 6, 7, 7, 23, 62, 143, 44, 159, 46, 47, 174, 2239, ... (OEIS A003458).
REFERENCES:
Ecklund, E. F. Jr.; Erdős, P.; and Selfridge, J. L. "A New Function Associated with the prime factors of 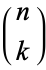 ." Math. Comput. 28, 647-649, 1974.
." Math. Comput. 28, 647-649, 1974.
Erdős, P.; Lacampagne, C. B.; and Selfridge, J. L. "Estimates of the Least Prime Factor of a Binomial Coefficient." Math. Comput. 61, 215-224, 1993.
Granville, A. and Ramare, O. "Explicit Bounds on Exponential Sums and the Scarcity of Squarefree Binomial Coefficients." Mathematika 43, 73-107, 1996.
Lukes, R. F.; Scheidler, R.; and Williams, H. C. "Further Tabulation of the Erdős-Selfridge Function." Math. Comput. 66, 1709-1717, 1997.
Scheidler, R. and Williams, H. C. "A Method of Tabulating the Number-Theoretic Function 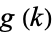 ." Math. Comput. 59, 251-257, 1992.
." Math. Comput. 59, 251-257, 1992.
Sloane, N. J. A. Sequence A003458/M2515 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|