


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-7-2020
Date: 17-3-2020
Date: 16-12-2020
|
The transformation ![S[{a_n}_(n=0)^N]](https://mathworld.wolfram.com/images/equations/StirlingTransform/Inline1.gif) of a sequence
of a sequence 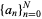 into a sequence
into a sequence 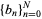 by the formula
by the formula
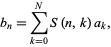 |
(1) |
where 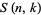 is a Stirling number of the second kind. The inverse transform is given by
is a Stirling number of the second kind. The inverse transform is given by
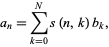 |
(2) |
where 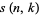 is a Stirling number of the first kind (Sloane and Plouffe 1995, p. 23).
is a Stirling number of the first kind (Sloane and Plouffe 1995, p. 23).
The following table summarized Stirling transforms for some common sequences, where ![[S]](https://mathworld.wolfram.com/images/equations/StirlingTransform/Inline6.gif) denotes the Iverson bracket and
denotes the Iverson bracket and 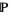 denotes the primes.
denotes the primes.
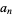 |
OEIS | ![S[{a_n}_(n=0)^N]](https://mathworld.wolfram.com/images/equations/StirlingTransform/Inline9.gif) |
| 1 | A000110 | 1, 1, 2, 5, 15, 52, 203, ... |
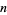 |
A005493 | 0, 1, 3, 10, 37, 151, 674, ... |
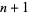 |
A000110 | 1, 2, 5, 15, 52, 203, 877, ... |
![[n in P]](https://mathworld.wolfram.com/images/equations/StirlingTransform/Inline12.gif) |
A085507 | 0, 0, 1, 4, 13, 41, 136, 505, ... |
![[n even]](https://mathworld.wolfram.com/images/equations/StirlingTransform/Inline13.gif) |
A024430 | 1, 0, 1, 3, 8, 25, 97, 434, 2095, ... |
![[n odd]](https://mathworld.wolfram.com/images/equations/StirlingTransform/Inline14.gif) |
A024429 | 0, 1, 1, 2, 7, 27, 106, 443, ... |
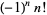 |
A033999 | 1, 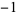 , 1, , 1, 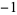 , 1, , 1, 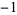 , ... , ... |
Here, ![S[{1}_(n=0)^N]](https://mathworld.wolfram.com/images/equations/StirlingTransform/Inline19.gif) gives the Bell numbers.
gives the Bell numbers.
![S[{n}_(n=0)^N]](https://mathworld.wolfram.com/images/equations/StirlingTransform/Inline20.gif) has the exponential generating function
has the exponential generating function
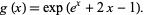 |
(3) |
REFERENCES:
Bernstein, M. and Sloane, N. J. A. "Some Canonical Sequences of Integers." Linear Algebra Appl. 226-228, 57-72, 1995.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Factorial Factors." §4.4 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, p. 252, 1994.
Riordan, J. Combinatorial Identities. New York: Wiley, p. 90, 1979.
Riordan, J. An Introduction to Combinatorial Analysis. New York: Wiley, p. 48, 1980.
Sloane, N. J. A. Sequences A000110/M1483, A005493/M2851, A024429, A024430, A033999, A052437, and A085507 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, 1995.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
المقابر الجماعية في العراق.. دراسة في القتل الجماعي والاختفاء القسري بحق الكثير من الأقليات والقوميات العرقية والدينية
|
|
|