المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Hofstadter Figure-Figure Sequence |
 931
 02:45 صباحاً
date: 28-10-2020 |
Author : Hofstadter, D. R. 
Book or Source : Gödel, Escher, Bach: An Eternal Golden Braid. New York: Vintage Books 
Page and Part : ...|
Read More
Date: 4-11-2020
687
Date: 14-11-2020
1123
Date: 21-10-2020
877
|
Define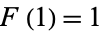 
and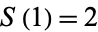 
and write
 |
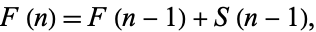where the sequence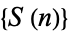 
consists of those integers not already contained in 
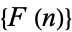. For example, 
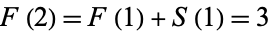, so the next term of 
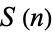is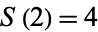 
, giving 
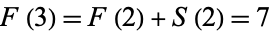. The next integer is 5, so 
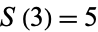and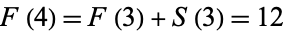 
. Continuing in this manner gives the "figure" sequence 
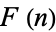as 1, 3, 7, 12, 18, 26, 35, 45, 56, ... (OEIS A005228) and the "space" sequence as 2, 4, 5, 6, 8, 9, 10, 11, 13, 14, ... (OEIS A030124).
REFERENCES:
Hofstadter, D. R. Gödel, Escher, Bach: An Eternal Golden Braid. New York: Vintage Books, p. 73, 1989.
Sloane, N. J. A. Sequences A005228/M2629 and A030124 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|
