


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-11-2020
Date: 1-8-2020
Date: 28-12-2020
|
A prime partition of a positive integer 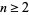 is a set of primes
is a set of primes 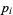 which sum to
which sum to 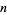 . For example, there are three prime partitions of 7 since
. For example, there are three prime partitions of 7 since
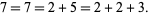 |
The number of prime partitions of 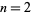 , 3, ... are 1, 1, 1, 2, 2, 3, 3, 4, 5, 6, 7, 9, 10, 12, 14, 17, 19, 23, 26, ... (OEIS A000607). If
, 3, ... are 1, 1, 1, 2, 2, 3, 3, 4, 5, 6, 7, 9, 10, 12, 14, 17, 19, 23, 26, ... (OEIS A000607). If 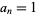 for
for 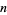 prime and
prime and 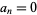 for
for 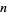 composite, then the Euler transform
composite, then the Euler transform 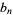 gives the number of partitions of
gives the number of partitions of 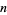 into prime parts (Sloane and Plouffe 1995, p. 21).
into prime parts (Sloane and Plouffe 1995, p. 21).
The minimum number of primes needed to sum to 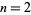 , 3, ... are 1, 1, 2, 1, 2, 1, 2, 2, 2, 1, 2, 1, 2, 2, 2, 1, 2, ... (OEIS A051034). The maximum number of primes needed to sum to
, 3, ... are 1, 1, 2, 1, 2, 1, 2, 2, 2, 1, 2, 1, 2, 2, 2, 1, 2, ... (OEIS A051034). The maximum number of primes needed to sum to 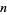 is just
is just 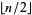 , 0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, ... (OEIS A004526), corresponding to a representation in terms of all 2s for an even number or one 3 and the rest 2s for an odd number.
, 0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, ... (OEIS A004526), corresponding to a representation in terms of all 2s for an even number or one 3 and the rest 2s for an odd number.
The numbers which can be represented by a single prime are obviously the primes themselves. Composite numbers which can be represented as the sum of two primes are 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, ... (OEIS A051035), and composite numbers which are not the sum of fewer than three primes are 27, 35, 51, 57, 65, 77, 87, 93, 95, 117, 119, ..., (OEIS A025583). The conjecture that no numbers require four or more primes is called the Goldbach conjecture.
REFERENCES:
Berndt, B. C. and Wilson, B. M. "Chapter 5 of Ramanujan's Second Notebook." In Analytic Number Theory: Proceedings of the Conference Held at Temple University, Philadelphia, Pa., May 12-15, 1980 (Ed. M. I. Knopp). Berlin: Springer-Verlag, pp. 49-78, 1981.
Chawla, L. M. and Shad, S. A. "On a Trio-Set of Partition Functions and Their Tables." J. Natural Sciences and Mathematics 9, 87-96, 1969.
Gupta, O. P. and Luthra, S. "Partitions into Primes." Proc. Nat. Inst. Sci. India. Part A 21, 181-184, 1955.
Gupta, H. "Partitions into Distinct Primes." Proc. Nat. Inst. Sci. India. Part A 21, 185-187, 1955.
Guy, R. K. "The Strong Law of Small Numbers." Amer. Math. Monthly 95, 697-712, 1988.
Sloane, N. J. A. Sequences A000607/M0265, A004526, A025583, A051034, and A051035 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, 1995.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|