


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-10-2020
Date: 5-11-2020
Date: 27-9-2020
|
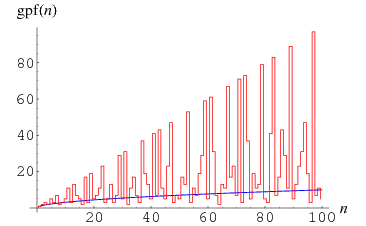
For an integer 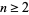 , let
, let 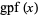 denote the greatest prime factor of
denote the greatest prime factor of 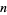 , i.e., the number
, i.e., the number 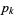 in the factorization
in the factorization
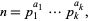 |
with 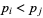 for
for 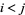 . For
. For 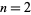 , 3, ..., the first few are 2, 3, 2, 5, 3, 7, 2, 3, 5, 11, 3, 13, 7, 5, ... (OEIS A006530). The greatest multiple prime factors for squareful integers are 2, 2, 3, 2, 2, 3, 2, 2, 5, 3, 2, 2, 3, ... (OEIS A046028).
, 3, ..., the first few are 2, 3, 2, 5, 3, 7, 2, 3, 5, 11, 3, 13, 7, 5, ... (OEIS A006530). The greatest multiple prime factors for squareful integers are 2, 2, 3, 2, 2, 3, 2, 2, 5, 3, 2, 2, 3, ... (OEIS A046028).
A number for which 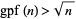 is called an unusual number by Greene and Knuth (1990) and a
is called an unusual number by Greene and Knuth (1990) and a 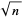 -rough numbers by Finch (2001). The first few
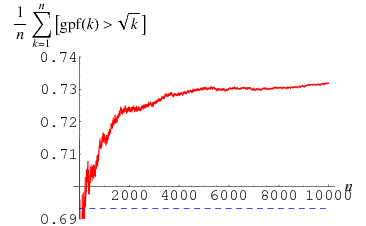
-rough numbers by Finch (2001). The first few 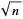 -rough numbers are 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 20, 21, ... (OEIS A064052). The probability that a random positive integer is
-rough numbers are 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 20, 21, ... (OEIS A064052). The probability that a random positive integer is 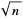 -rough is
-rough is 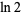 (Schroeppel 1972).
(Schroeppel 1972).
A number that is not 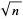 -rough is called, not surprisingly, a
-rough is called, not surprisingly, a 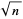 -smooth number (or sometimes, a "round number"). The first few are 1, 4, 8, 9, 12, 16, 18, 24, 25, 27, ... (OEIS A048098).
-smooth number (or sometimes, a "round number"). The first few are 1, 4, 8, 9, 12, 16, 18, 24, 25, 27, ... (OEIS A048098).
REFERENCES:
Erdős, P. and Pomerance, C. "On the Largest Prime Factors of 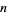 and
and 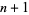 ." Aequationes Math. 17, 211-321, 1978.
." Aequationes Math. 17, 211-321, 1978.
Finch, S. "RE: Unusual Numbers." 27 Aug 2001. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0108&L=nmbrthry&P=963.
Greene, D. H. and Knuth, D. E. Mathematics for the Analysis of Algorithms, 3rd ed. Boston, MA: Birkhäuser, 1990.
Guy, R. K. "The Largest Prime Factor of 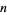 ." §B46 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 101, 1994.
." §B46 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 101, 1994.
Heath-Brown, D. R. "The Largest Prime Factor of the Integers in an Interval." Sci. China Ser. A 39, 449-476, 1996.
Mahler, K. "On the Greatest Prime Factor of 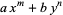 ." Nieuw Arch. Wisk. 1, 113-122, 1953.
." Nieuw Arch. Wisk. 1, 113-122, 1953.
Schroeppel, R. Item 29 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 13, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item29.
Sloane, N. J. A. Sequences A006530/M0428, A048098, and A064052 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|