Cofactor

Given a factor 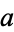 of a number 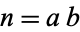, the cofactor of  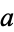is .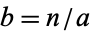

A different type of cofactor, sometimes called a cofactor matrix, is a signed version of a minor 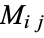 defined by

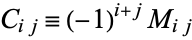and used in the computation of the determinant of a matrix 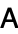 according to

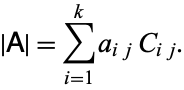The cofactor can be computed in the Wolfram Language using

  Cofactor[m_List?MatrixQ, {i_Integer, j_Integer}] :=
    (-1)^(i+j) Det[Drop[Transpose[
      Drop[Transpose[m], {j}]], {i}
    ]]

which is the equivalent of the 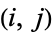th component of the CofactorMatrix defined below.

  MinorMatrix[m_List?MatrixQ] :=
    Map[Reverse, Minors[m], {0, 1}]
  CofactorMatrix[m_List?MatrixQ] :=
    MapIndexed[#1 (-1)^(Plus @@ #2)&,
      MinorMatrix[m],{2}]

Cofactors can be computed using Cofactor[m, 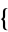i, j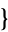] in the Wolfram Language package Combinatorica` .

REFERENCES:

 Lichtblau, D. "Symbolic FAQ." https://library.wolfram.com/infocenter/Conferences/325.

Muir, T. A Treatise on the Theory of Determinants. New York: Dover, p. 54, 1960.

Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, p. 235, 1990.