Brent's Factorization Method

The second part of Pollard rho factorization method concerns detection of the fact that a sequence has become periodic. Pollard's original suggestion was to use the idea attributed to Floyd of comparing 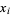 to 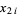 for all 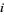. Brent's improvement to Pollard's method concerns how to detect periodicity, and replaces Floyd's method with the following algorithm. Keep only one running copy o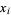f . If 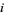 is a power of a base 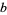, let 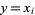, and at each step, compare the current value  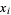with the saved value 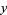. In the factorization case, instead of comparing  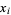with 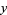, compute

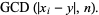More generally, Brent (1980) considered using any base 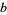 for saving values instead of 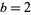. However, he found  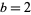to be very close to optimal.

REFERENCES:

Brent, R. "An Improved Monte Carlo Factorization Algorithm." Nordisk Tidskrift for Informationsbehandlung (BIT) 20, 176-184, 1980.