Dirichlet's Theorem

Given an arithmetic progression of terms 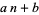, for 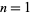, 2, ..., the series contains an infinite number of primes if  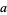and 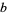 are relatively prime, i.e., 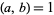. This result had been conjectured by Gauss (Derbyshire 2004, p. 96), but was first proved by Dirichlet (1837).

Dirichlet proved this theorem using Dirichlet L-series, but the proof is challenging enough that, in their classic text on number theory, the usually explicit Hardy and Wright (1979) report "this theorem is too difficult for insertion in this book."

REFERENCES:

Courant, R. and Robbins, H. "Primes in Arithmetical Progressions." §1.2b in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 26-27, 1996.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 95-97, 2004.

Dirichlet, L. "Beweis des Satzes, dass jede unbegrenzte arithmetische Progression, deren erstes Glied und Differenz ganze Zahlen ohne gemeinschaftlichen Factor sing, unendlich viele Primzahlen erhält." Abhandlungen der Königlich Preussischen Akademie der Wissenschaften, pp. 45-81, 1837.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 13-14, 1979.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 186, 2003.

Landau, E. Vorlesungen über Zahlentheorie, Vol. 1. New York: Chelsea, pp. 79-96, 1970.

Landau, E. Handbuch der Lehre von der Verteilung der Primzahlen, 3rd ed. New York: Chelsea, pp. 422-446, 1974.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 22-23, 1993.