


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-8-2020
Date: 8-11-2020
Date: 4-11-2020
|
There are two problems commonly known as the subset sum problem.
The first ("given sum problem") is the problem of finding what subset of a list of integers has a given sum, which is an integer relation problem where the relation coefficients 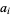 are 0 or 1.
are 0 or 1.
The ("same sum problem") is the problem of finding a set of 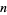 distinct positive real numbers with as large a collection as possible of subsets with the same sum (Proctor 1982).
distinct positive real numbers with as large a collection as possible of subsets with the same sum (Proctor 1982).
The same sum problem was solved by Stanley (1980) using the tools of algebraic geometry, with the answer given for 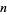 numbers by the first
numbers by the first 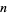 positive integers:
positive integers: 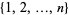 . Proctor (1982) gave the first elementary proof of this result. The maximal numbers of subsets of
. Proctor (1982) gave the first elementary proof of this result. The maximal numbers of subsets of 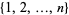 having the same sum for
having the same sum for 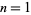 , 2, ... are 1, 1, 2, 2, 3, 5, 8, 14, 23, ... (OEIS A025591). Similarly, the numbers of different subset sums for
, 2, ... are 1, 1, 2, 2, 3, 5, 8, 14, 23, ... (OEIS A025591). Similarly, the numbers of different subset sums for 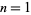 , 2, ... are 2, 4, 7, 11, 16, 22, 29, 37, 46, 56, ... (OEIS A000124). For example, for
, 2, ... are 2, 4, 7, 11, 16, 22, 29, 37, 46, 56, ... (OEIS A000124). For example, for 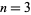 , the subsets of
, the subsets of 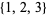 are
are
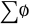 |
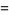 |
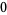 |
(1) |
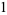 |
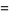 |
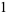 |
(2) |
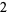 |
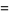 |
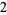 |
(3) |
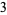 |
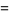 |
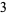 |
(4) |
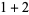 |
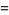 |
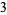 |
(5) |
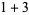 |
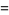 |
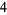 |
(6) |
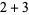 |
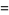 |
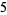 |
(7) |
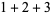 |
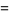 |
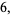 |
(8) |
so the sum appearing most often is 3, which occurs twice, and the number of different sums is 7.
The given sum problem is NP-complete. For small cases, it be solved using generating functions. Consider the number of ways 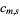 to select
to select 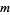 out of
out of 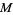 given integers
given integers 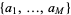 such that their sum equals
such that their sum equals 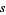 , and define the generating function
, and define the generating function
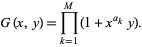 |
(9) |
Upon expanding in powers of 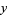 , this becomes
, this becomes
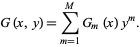 |
(10) |
But as a result of the exponent law 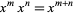 ,
, 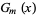 is precisely the desired generating function
is precisely the desired generating function
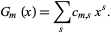 |
(11) |
For example, consider the problem of picking 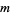 objects from the set
objects from the set 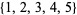 . The generating function
. The generating function 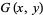 is
is
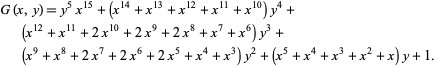 |
(12) |
So, for example, selecting 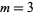 objects has the generating function
objects has the generating function
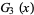 |
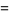 |
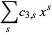 |
(13) |
 |
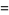 |
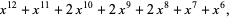 |
(14) |
so the number of ways of picking three of the integers 1 through 5 and having them sum to 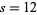 , 11, ..., 6 are the coefficients
, 11, ..., 6 are the coefficients 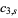 of
of 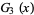 , namely 1, 1, 2, 2, 2, 1, and 1. These solutions are summarized in the following table.
, namely 1, 1, 2, 2, 2, 1, and 1. These solutions are summarized in the following table.
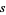 |
solutions |
| 6 | (1, 2, 3) |
| 7 | (1, 2, 4) |
| 8 | (1, 2, 5), (1, 3, 4) |
| 9 | (1, 3, 5), (2, 3, 4) |
| 10 | (1, 4, 5), (2, 3, 5) |
| 11 | (2, 4, 5) |
| 12 | (3, 4, 5) |
A nice explicit example original proposed by Pólya (1956) asks for the number of ways to make change from an American dollar (using pennies, nickels, dimes, quarters, and half-dollars). The answer of 292 is provided as the coefficient of the 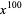 term in the series
term in the series
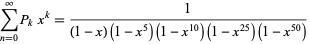 |
(15) |
(Borwein and Bailey 2003, p. 21).
REFERENCES:
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 22-24, 2003.
Coster, M. J.; LaMacchia, B. A.; Odlyzko, A. M.; and Schnorr, C. P. "An Improved Low-Density Subset Sum Algorithm." In Advances in Cryptology: EUROCRYPT '91 (Brighton, 1999) (Ed. D. W. Davis). New York: Springer-Verlag, pp. 54-67, 1992.
Coster, M. J.; Joux, A.; LaMacchia, B. A.; Odlyzko, A. M.; Schnorr, C. P.; and Stern, J. "Improved Low-Density Subset Sum Algorithms." Comput. Complex. 2, 111-128, 1992.
Ferguson, H. R. P. and Bailey, D. H. "A Polynomial Time, Numerically Stable Integer Relation Algorithm." RNR Techn. Rept. RNR-91-032, Jul. 14, 1992.
Lagarias, L. C. and Odlyzko, A. M. "Solving Low-Density Subset Sum Problems." J. ACM 32, 229-246, 1985.
Pólya, G. "On Picture-Writing." Amer. Math. Monthly 63, 689-697, 1956.
Proctor, R. A. "Solution of Two Difficult Combinatorial Problems with Linear Algebra." Amer. Math. Monthly 89, 721-734, 1982.
Schnorr, C. P. and Euchner, M. "Lattice Basis Reduction: Improved Practical Algorithms and Solving Subset Sum Problems." In Fundamentals of Computation Theory: Proceedings of the 8th International Conference, Fct '91 Gosen, Germany, September 9-13, 1991. Berlin: Springer-Verlag, pp. 68-85, 1991.
Sloane, N. J. A. Sequences A000124/M1041 and A025591 in "The On-Line Encyclopedia of Integer Sequences."
Stanley, R. P. "Weyl Groups, the Hard Lefschetz Theorem, and the Sperner Property." SIAM J. Alg. Disc. Math. 1, 168-184, 1980.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|