Euler-Mascheroni Constant Continued Fraction

The simple continued fraction of the Euler-Mascheroni constant  is [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, ...] (OEIS A002852). The first few convergents are 1, 1/2, 3/5, 4/7, 11/19, 15/26, 71/123, 228/395, 3035/5258, 15403/26685, ... (OEIS A046114 and A046115), which are good to 0, 0, 1, 1, 2, 2, 3, 4, 6, 8, 9, 9, 10, ... (OEIS A114541) decimal digits, respectively.

The following table summarizes some record computations of the continued fraction of .

terms	date	reference
	Sep. 21, 2011	E. W. Weisstein
	Jul. 22, 2013	E. W. Weisstein

The plot above shows the positions of the first occurrences of 1, 2, 3, ... in the continued fraction, the first few of which are 1, 3, 8, 7, 10, 68, 23, 13, 138, 51, 21, ... (OEIS A224847). The smallest positive integers not appearing in the first  terms of the continued fraction are 27943, 33436, 33978, 34017, ... (E. W. Weisstein, Jul. 22, 2013).

The sequence of largest terms in the continued fraction is 1, 2, 4, 13, 40, 49, 65, 399, 2076, ... (OEIS A033091), which occur at positions 1, 3, 7, 9, 19, 30, 33, 39, 528, ... (OEIS A224849).

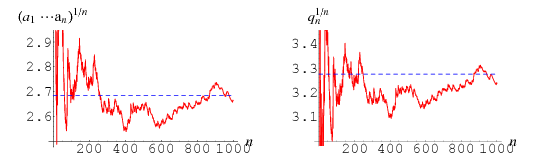
Let the continued fraction of  be denoted  and let the denominators of the convergents be denoted , , ..., . Then plots above show successive values of , , , which appear to converge to Khinchin's constant (left figure) and , which appear to converge to the Lévy constant (right figure), although neither of these limits has been rigorously established.

REFERENCES:

Sloane, N. J. A. Sequences A002852/M0097, A033091, A046114, A046115, A114541, A224847, and A224849 in "The On-Line Encyclopedia of Integer Sequences."