المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Murata,s Constant |
 513
 03:19 مساءً
date: 19-3-2020 |
Author : Murata, L. 
Book or Source : "On the Magnitude of the Least Prime Primitive Root." J. Number Th. 37 
Page and Part : ...|
Read More
Date: 13-11-2019
754
Date: 15-9-2020
1060
Date: 4-5-2020
727
|
Murata's constant is defined as
 |
 |
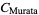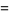![product_(p)[1+1/((p-1)^2)]](https://mathworld.wolfram.com/images/equations/MuratasConstant/Inline3.gif) |
(1) |
 |
 |
 |
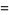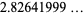(2) |
(OEIS A065485), where the product is over the primes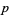 
. It can also be written as the sum
 |
 |
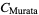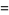![exp[-sum_(n=2)^(infty)((1+i)^n+(1-i)^n-2)/nP(n)]](https://mathworld.wolfram.com/images/equations/MuratasConstant/Inline10.gif) |
(3) |
 |
 |
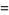![exp[sum_(n=2)^(infty)(2-2^(n/2+1)cos(1/4npi))/nP(n)],](https://mathworld.wolfram.com/images/equations/MuratasConstant/Inline13.gif) |
(4) |
where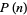 
is the prime zeta function.
REFERENCES:
Finch, S. R. "Artin's Constant." §2.4 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 104-106, 2003.
Murata, L. "On the Magnitude of the Least Prime Primitive Root." J. Number Th. 37, 47-66, 1991.
Niklasch, G. "Some Number-Theoretical Constants." http://www.gn-50uma.de/alula/essays/Moree/Moree.en.shtml.
Sloane, N. J. A. Sequence A065485 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|
