


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-12-2019
Date: 18-8-2020
Date: 5-9-2020
|
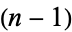 -digit integer that, when multiplied by 1, 2, 3, ...,
-digit integer that, when multiplied by 1, 2, 3, ..., 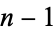 , produces the same digits in a different order. Cyclic numbers are generated by the full reptend primes, i.e., 7, 17, 19, 23, 29, 47, 59, 61, 97, ... (OEIS A001913).
, produces the same digits in a different order. Cyclic numbers are generated by the full reptend primes, i.e., 7, 17, 19, 23, 29, 47, 59, 61, 97, ... (OEIS A001913).
The decimal expansions giving the first few cyclic numbers are
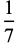 |
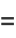 |
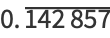 |
(1) |
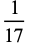 |
 |
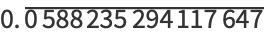 |
(2) |
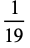 |
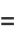 |
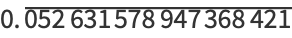 |
(3) |
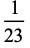 |
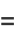 |
 |
(4) |
(OEIS A004042).
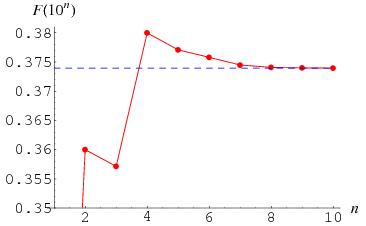
The numbers of cyclic numbers 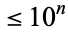 for
for 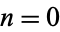 , 1, 2, ... are 0, 1, 9, 60, 467, 3617, 25883, 248881, 2165288, 19016617, 170169241, ... (OEIS A086018). It has been conjectured, but not yet proven, that an infinite number of cyclic numbers exist. In fact, the fraction of cyclic numbers out of all primes has been conjectured to be Artin's constant
, 1, 2, ... are 0, 1, 9, 60, 467, 3617, 25883, 248881, 2165288, 19016617, 170169241, ... (OEIS A086018). It has been conjectured, but not yet proven, that an infinite number of cyclic numbers exist. In fact, the fraction of cyclic numbers out of all primes has been conjectured to be Artin's constant 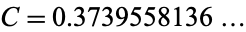 . The fraction of cyclic numbers among primes
. The fraction of cyclic numbers among primes 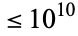 is 0.3739551.
is 0.3739551.
When a cyclic number is multiplied by its generator, the result is a string of 9s. This is a special case of Midy's theorem.
See Yates (1973) for a table of prime period lengths for primes 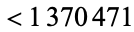 .
.
REFERENCES:
Gardner, M. "Cyclic Numbers." Ch. 10 in Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments from Scientific American. New York: Knopf, pp. 111-122, 1979.
Guttman, S. "On Cyclic Numbers." Amer. Math. Monthly 44, 159-166, 1934.
Kraitchik, M. "Cyclic Numbers." §3.7 in Mathematical Recreations. New York: W. W. Norton, pp. 75-76, 1942.
Rao, K. S. "A Note on the Recurring Period of the Reciprocal of an Odd Number." Amer. Math. Monthly 62, 484-487, 1955.
Rivera, C. "Problems & Puzzles: Puzzle 012-Period Length of 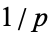 ." http://www.primepuzzles.net/puzzles/puzz_012.htm.
." http://www.primepuzzles.net/puzzles/puzz_012.htm.
Sloane, N. J. A. Sequences A001913/M4353, A004042, and A086018 in "The On-Line Encyclopedia of Integer Sequences."
Yates, S. Primes with Given Period Length. Trondheim, Norway: Universitetsforlaget, 1973.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|